Question

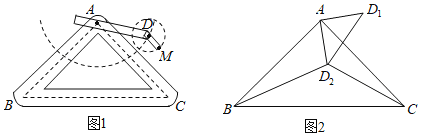
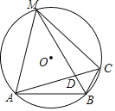
【题目】如图，在⊙O中，B是⊙O上的一点，∠ABC＝120°，弦AC＝，弦BM平分∠ABC交AC于点D，连接MA，MC．

（1）试判断的形状；

（2）求⊙O半径的长.

Answer 1

【答案】（1）等边三角形；（2）2.

【解析】

（1）由角平分线的性质可得∠ABM=∠CBM=60°,根据等弧对等角可得∠MAC=∠MBC=60°, ∠MCA=∠MBA=60°,进而可得为等边三角形；

（2）过点O作OH⊥AC于H,连接AO,CO，易知∠AOC=2∠AMC=120°,由垂径定理可得∠AOH=60°,AH=,然后解直角三角形可得AO的长度.

（1）∵∠ABC＝120°，弦BM平分∠ABC，

∴∠ABM=∠CBM=60°,

∴∠MAC=∠MBC=60°, ∠MCA=∠MBA=60°,

∴为等边三角形；

（2）过点O作OH⊥AC于H,连接AO,CO.

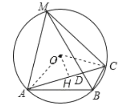
∵为等边三角形

∴∠AMC=60°,

∴∠AOC=2∠AMC=120°,

∵OH⊥AC,OA=OC,

∴∠AOH=60°,AH=AC=,

在中，sin∠AOH=

∴AO===2,

∴⊙O的半径为2.