题目内容
11.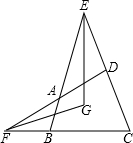 如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADC=60°,∠ABC=80°.
如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADC=60°,∠ABC=80°.(1)求∠EGF的大小.
(2)猜想∠EGF与∠ADC,∠ABC的数量关系.
分析 (1)首先在图形上添加∠1、∠2、∠3、∠4,然后根据角之间的关系进行解答;
(2)根据(1)得出其关系即可.
解答 解:(1)添加∠1、∠2、∠3、∠4,如右图,
∵∠1=60°-∠AED,∠FAB=80°-∠AFB,
∴2∠4=360°-∠1-∠FAB=360°-(60°-∠AED)-(80°-∠AFB)=220°+∠AED+∠AFB,
∴∠4=110°+$\frac{1}{2}$∠AED+$\frac{1}{2}$∠AFB,
∴∠2=60°-$\frac{1}{2}$∠AEC,∠3=80°-$\frac{1}{2}$∠AFB,
∴∠EGF=360°-(∠4+∠2+∠3),
=360°-110°-$\frac{1}{2}$∠AED-$\frac{1}{2}$∠AFB-60°+$\frac{1}{2}$∠AED-80°+$\frac{1}{2}$∠AFB
=360°-110°-60°-80°
=110°;
(2)根据(1)中可得∠EGF=180°-$\frac{1}{2}$(∠ADC+∠ABC).
点评 本题考查角与角之间的运算,注意结合图形,发现角与角之间的关系,进而求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.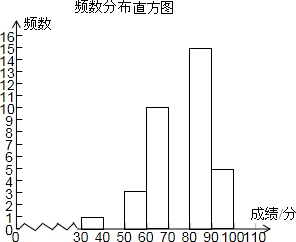 如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
频数分布表
(1)以上分组的组距=10
(2)请补全频数分布表和频数分布直方图;
(3)请计算这50名同学的平均成绩;
(4)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
 如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.频数分布表
| 成绩分组 | 频数 | 频率 |
| 30≤x<40 | 1 | 0.02 |
| 40≤x<50 | 1 | 0.02 |
| 50≤x<60 | 3 | 0.06 |
| 60≤x<70 | 10 | 0.2 |
| 70≤x<80 | 15 | 0.3 |
| 80≤x<90 | 15 | 0.3 |
| 90≤x<100 | 5 | 0.1 |
| 合计 | 50 | 1 |
(2)请补全频数分布表和频数分布直方图;
(3)请计算这50名同学的平均成绩;
(4)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
16.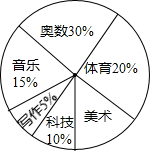 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
(1)七年级共有学生360人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是63;
(4)众数是72.
 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.| 学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
| 人数 | 72 | 36 | 54 | 18 |
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是63;
(4)众数是72.
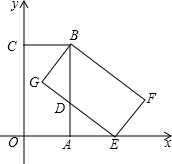 如图,已知在直角坐标系中,矩形OABC的边OA在x轴正半轴上,边OC在y轴的正半轴上,B点的坐标为(4,8),将矩形OABC绕点B逆时针旋转得到矩形EFBG,点E恰好落在x轴上.
如图,已知在直角坐标系中,矩形OABC的边OA在x轴正半轴上,边OC在y轴的正半轴上,B点的坐标为(4,8),将矩形OABC绕点B逆时针旋转得到矩形EFBG,点E恰好落在x轴上.



 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2,则△ABC的面积=$\frac{2\sqrt{3}}{3}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2,则△ABC的面积=$\frac{2\sqrt{3}}{3}$.