题目内容
(1)已知x≠1,计算(1-x)(1+x)= ,(1-x)(1+x+x2)= ,(1-x)(1+x+x2+x3)= ,观察上式,猜想(1-x)(1+x+x2+…+xn)= .
(2)已知a≠b,则(a2-b2)÷(a-b)= ,(a3-b3)(a-b)= .
利用上题结果猜想(a4-b4)÷(a-b)的结果并检验猜想是否正确?
(2)已知a≠b,则(a2-b2)÷(a-b)=
利用上题结果猜想(a4-b4)÷(a-b)的结果并检验猜想是否正确?
考点:整式的混合运算
专题:规律型
分析:(1)利用多项式乘以多项式法则计算,归纳总结得到一般性规律,写出即可;
(2)利用多项式除以多项式法则计算得到结果,归纳总结出一般性结论,猜想(a4-b4)÷(a-b)的结果,验证即可.
(2)利用多项式除以多项式法则计算得到结果,归纳总结出一般性结论,猜想(a4-b4)÷(a-b)的结果,验证即可.
解答:解:(1)已知x≠1,计算(1-x)(1+x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4,
观察上式,猜想(1-x)(1+x+x2+…+xn)=1-xn+1;
(2)已知a≠b,则(a2-b2)÷(a-b)=a+b,(a3-b3)(a-b)=a2+ab+b2;
利用上题结果猜想(a4-b4)÷(a-b)=a3+ab2+a2b+b3,
证明:(a4-b4)÷(a-b)
=(a-b)(a+b)(a2+b2)÷(a-b)
=(a+b)(a2+b2)
=a3+ab2+a2b+b3.
故答案为:(1)1-x2;1-x3;1-x4;1-xn+1;(2)a+b;a2+ab+b2
观察上式,猜想(1-x)(1+x+x2+…+xn)=1-xn+1;
(2)已知a≠b,则(a2-b2)÷(a-b)=a+b,(a3-b3)(a-b)=a2+ab+b2;
利用上题结果猜想(a4-b4)÷(a-b)=a3+ab2+a2b+b3,
证明:(a4-b4)÷(a-b)
=(a-b)(a+b)(a2+b2)÷(a-b)
=(a+b)(a2+b2)
=a3+ab2+a2b+b3.
故答案为:(1)1-x2;1-x3;1-x4;1-xn+1;(2)a+b;a2+ab+b2
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16位参加百米决赛同学的成绩各不相同,按成绩取前8位进入决赛,如果小刘知道了自己的成绩后,要判断能否进入决赛,其他15位同学成绩的下列数据中,能使他得出结论的是( )
| A、中位数 | B、众数 |
| C、平均数 | D、加权平均数 |
一元二次方程x2-9=0的解是( )
| A、x=-3 |
| B、x=3 |
| C、x1=3,x2=-3 |
| D、x=81 |
下列图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )
如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
 如图,在平行四边形ABCD中,BE与CF分别平分∠ABC和∠BCD,交AD于E和两点,已知AD的长为8cm,EF的长为2cm,则AB的长为
如图,在平行四边形ABCD中,BE与CF分别平分∠ABC和∠BCD,交AD于E和两点,已知AD的长为8cm,EF的长为2cm,则AB的长为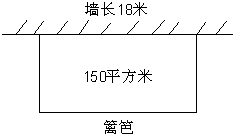 如图,有一面积为150m2的长方形鸡场,鸡场的一边靠墙(墙长18m),另三边用竹篱笆围成,如果竹篱笆的长为35m,
如图,有一面积为150m2的长方形鸡场,鸡场的一边靠墙(墙长18m),另三边用竹篱笆围成,如果竹篱笆的长为35m,