题目内容
1.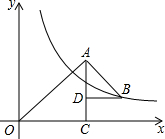 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=14,则k的值是7.
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=14,则k的值是7.
分析 由△OAC和△BAD都是等腰直角三角形,可设设OC=a,AD=b,由此得出“AC=a,OA=$\sqrt{2}$a,BD=b,AB=$\sqrt{2}$b”,结合OA2-AB2=14,可得出a2-b2=7,结合图象找出点B的坐标,结合反比例函数图象上点的坐标特征即可得出结论.
解答 解:∵△OAC和△BAD都是等腰直角三角形,
∴设OC=a,AD=b,则AC=a,OA=$\sqrt{2}$a,BD=b,AB=$\sqrt{2}$b,
又∵OA2-AB2=14,
∴2(a2-b2)=14,a2-b2=7.
∵点B的坐标为(a+b,a-b),
∴k=(a+b)(a-b)=a2-b2=7.
故答案为:7.
点评 本题考查了反比例函数图象上点的坐标特征以及等腰直角三角形的性质,解题的关键是找出a2-b2=7.本题属于基础题,难度不大,解决该题型题目时,根据线段间的关系找出点B的坐标是关键.

练习册系列答案
相关题目
9. 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )
 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
13.近阶段潍坊持续干旱,给居民生活带来不便,关注水龙头的浪费十分必要,假设20滴水1毫升,一分钟浪费60滴,一年按365天计算,一年浪费水的质量用科学记数法表示为( )克(保留3个有效数字)
| A. | 1.60×106 | B. | 1.57×106 | C. | 1.58×106 | D. | 1.58×105 |
11.在0,-2,2,-3这四个数中,最小的数是( )
| A. | 0 | B. | -2 | C. | 1 | D. | -3 |
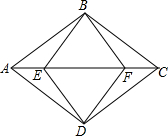 如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.