题目内容
4.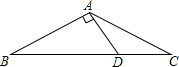 如图,在△ABC中,AB=AC,AD⊥AB交BC于点D,∠CAD=30°.
如图,在△ABC中,AB=AC,AD⊥AB交BC于点D,∠CAD=30°.(1)求证:BD=2CD;
(2)取BD的中点E,连接AE,求证:△ADE为等边三角形.
分析 (1)根据已知条件AB=AC,∠CAD=30°,AD⊥AB,得到∠BAC=120°,根据三角形的内角和得到∠B=∠C=∠CAD=30°,证得AD=CD,然后根据直角三角形的性质即可得到结论;
(2)根据直角三角形的性质得到AE=BE=DE,根据三角形的内角和得到∠ADE=60°,于是证得结论.
解答 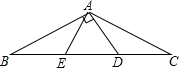 (1)证明:∵AB=AC,∠CAD=30°,AD⊥AB,
(1)证明:∵AB=AC,∠CAD=30°,AD⊥AB,
∴∠BAC=120°,
∴∠B=∠C=∠CAD=30°,
∴AD=CD,
∴BD=2AD=2CD;
(2)解:如图,∵点E是BD的中点,∠BAD=90°,
∴AE=BE=DE,
∵∠B=30°,
∴∠ADE=60°,
∴△ADE是等边三角形.
点评 本题考查了直角三角形的性质,等边三角形的判定,熟练掌握各定理是解题的关键.

练习册系列答案
相关题目
9.在△ABC中,∠C=90°.若AC=$\frac{\sqrt{2}}{2}$,tanA=1,则AB等于( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
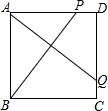 如图,A、B、C、D四家工厂分别坐落在正方形城镇的四个角上,仓库P和Q分别位于AD和DC上,且PD=QC,证明两条直路BP=AQ且BP⊥AQ.
如图,A、B、C、D四家工厂分别坐落在正方形城镇的四个角上,仓库P和Q分别位于AD和DC上,且PD=QC,证明两条直路BP=AQ且BP⊥AQ.