题目内容
13.由山脚下的一点A测得山顶D的仰角是45°,从A沿斜坡AB(坡角∠BAC=30°)前进100米到B,再次测得山顶D的仰角是60°,求山高CD.分析 首先根据题意分析图形;过点B作CD,AC的垂线,垂足分别为E,F,构造两个直角三角形△ABF与△BDE,分别求解可得DF与EB的值,再利用图形关系,进而可求出答案.
解答 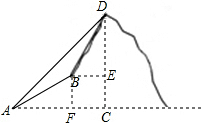 解:过点B作CD,AC的垂线,垂足分别为E,F,
解:过点B作CD,AC的垂线,垂足分别为E,F,
∵∠BAC=30°,AB=100米,
∴BF=EC=50米.
AF=AB•cos∠BAC=100×$\frac{\sqrt{3}}{2}$=50$\sqrt{3}$(米).
设FC=x米,
∵∠DBE=60°,
∴DE=$\sqrt{3}$x米.
又∵∠DAC=45°,
∴AC=CD.
即:50$\sqrt{3}$+x=50+$\sqrt{3}$x,
解得x=50.
则CD=50($\sqrt{3}$+1)米.
即山高为50($\sqrt{3}$+1)米.
点评 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
8.为满足学生业余时间读书,学校图书馆添置图书,用240元购进一种科普书,同时用200元购进一种文学书,已知科普书的单价比文学书的单价高出一半,所以购进的文学书比科普书多4本.若设这种文学书的单价为x元,下列所列方程正确的是( )
| A. | $\frac{1.5×200}{x}$-$\frac{240}{x}$=4 | B. | $\frac{240}{1.5x}$-$\frac{200}{4}$=4 | ||
| C. | $\frac{200}{x}$-$\frac{240}{1.5x}$=4 | D. | $\frac{1.5x+200}{x+4}$=$\frac{240}{x}$ |
18.(-16)2的算术平方根是( )
| A. | 16 | B. | 4 | C. | ±16 | D. | ±4 |
3.与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{8}$ | C. | $\sqrt{12}$ | D. | $\sqrt{20}$ |
 如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.
如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点. 在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3),B(3,1),O(0,0).
在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3),B(3,1),O(0,0).