题目内容
5．（1）解方程：x2+4x-2=0；（2）解不等式组：$\left\{\begin{array}{l}x-3（x-2）≥2\\ 4x-2＜5x+1\end{array}\right.$．
分析 （1）求出b2-4ac的解集，再根据找不等式组解集的规律找出不等式组的解集即可；
（2）先求出每个不等式的解集，再根据找不等式组解集的规律找出不等式组的解集即可．
解答 解：（1）x2+4x-2=0，
b2-4ac=42-4×1×（-2）=24，
x=$\frac{-4±\sqrt{24}}{2}$，
x1=-2+$\sqrt{6}$，x2=-2-$\sqrt{6}$；
（2）$\left\{\begin{array}{l}{x-3（x-2）≥2①}\\{4x-2＜5x+1②}\end{array}\right.$
∵解不等式①得：x≤2，
解不等式②得：x＞-3，
∴不等式组的解集为-3＜x≤2．
点评 本题考查了解一元一次不等式组，解一元二次方程的应用，能选择适当的方法解一元二次方程是解（1）的关键，能根据不等式的解集找出不等式组的解集是解（2）的关键．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
20．若二次函数y=ax2+bx+c的图象与x轴有两个交点，坐标为A（m，0），B（n，0），且m＜n，图象上有一点C（3，P）在x轴下方，则下列判断正确的是（ ）
| A． | b2-4ac≥0 | B． | m＜3＜n | C． | （m-3）（n-3）＜0 | D． | 以上都不对 |
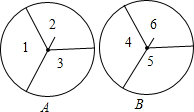有两个可以自由转动的均匀转盘A．B，都被分成3等份，并在每份内均标有数字，如图所示，规则如下：①分别转动转盘A．B，②两个转盘停止后，将两个指针所指份内的数字相乘（若指针停止在等份线上，那么重转一次，直到指针指向某 一份为止）．