题目内容
 如图,⊙P与两坐标轴分别交于点A(-2、0)、B(-6、0)、C(0、-3)和点D,双曲线
如图,⊙P与两坐标轴分别交于点A(-2、0)、B(-6、0)、C(0、-3)和点D,双曲线 过点P,则k=________.
过点P,则k=________.
14
分析:解双曲线方程时,只需要求得此双曲线上的一个点的坐标即可,由题设条件可知,双曲线过点P,所以由题设条件求出圆心坐标P即可.
解答: 解:如图,P点为圆心,是AB与AC两中垂线的交点.分别作AB与AC的中垂线PE与PQ.
解:如图,P点为圆心,是AB与AC两中垂线的交点.分别作AB与AC的中垂线PE与PQ.
E点为AB中点,其坐标为:(-4,0)
Q点为AC中点,其坐标为:(-1,- )
)
PE⊥x轴,∴px=-4.

PQ⊥AC,∴
直线PQ的方程为:
代入px=-4得:
将P点坐标代入双曲线方程得:
k=(-4)×(- )=14.
)=14.
点评:此题综合考查了圆心的确定方法及用待定系数法确定反比例函数的比例系数k,解题时要细心,防止出错.
分析:解双曲线方程时,只需要求得此双曲线上的一个点的坐标即可,由题设条件可知,双曲线过点P,所以由题设条件求出圆心坐标P即可.
解答:
 解:如图,P点为圆心,是AB与AC两中垂线的交点.分别作AB与AC的中垂线PE与PQ.
解:如图,P点为圆心,是AB与AC两中垂线的交点.分别作AB与AC的中垂线PE与PQ.E点为AB中点,其坐标为:(-4,0)
Q点为AC中点,其坐标为:(-1,-
 )
)PE⊥x轴,∴px=-4.

PQ⊥AC,∴

直线PQ的方程为:

代入px=-4得:

将P点坐标代入双曲线方程得:
k=(-4)×(-
 )=14.
)=14.点评:此题综合考查了圆心的确定方法及用待定系数法确定反比例函数的比例系数k,解题时要细心,防止出错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
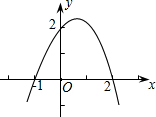 如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当y>2时,自变量x的取值范围是( )
如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当y>2时,自变量x的取值范围是( )A、0<x<
| ||
| B、0<x<1 | ||
C、
| ||
| D、-1<x<2 |
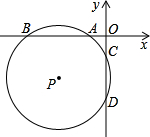 如图,⊙P与两坐标轴分别交于点A(-2、0)、B(-6、0)、C(0、-3)和点D,双曲线
如图,⊙P与两坐标轴分别交于点A(-2、0)、B(-6、0)、C(0、-3)和点D,双曲线 如图,⊙M与两坐标轴交于点A(-2,0)、B(6,0)、C(0,4)三点,且双曲线经过点M,则其双曲线的解析式为
如图,⊙M与两坐标轴交于点A(-2,0)、B(6,0)、C(0,4)三点,且双曲线经过点M,则其双曲线的解析式为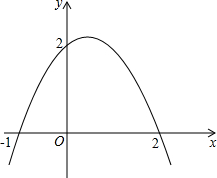 (2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),
(2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2), 如图:一次函数与两坐标轴交于A,B两点,与反比例函数交于C,D两点,已知点A(2,0)且OA=OB=AC=BD,求一次函数与反比例函数的解析式.
如图:一次函数与两坐标轴交于A,B两点,与反比例函数交于C,D两点,已知点A(2,0)且OA=OB=AC=BD,求一次函数与反比例函数的解析式.