题目内容
 如图,⊙M与两坐标轴交于点A(-2,0)、B(6,0)、C(0,4)三点,且双曲线经过点M,则其双曲线的解析式为
如图,⊙M与两坐标轴交于点A(-2,0)、B(6,0)、C(0,4)三点,且双曲线经过点M,则其双曲线的解析式为分析:过点M作ME⊥x轴,MF⊥y轴,垂足为E、F,连接MB、MC,由垂径定理可知BE=
AB=4,故OE=MF=OB-BE=2,设OF=ME=b,则FC=4-b,在Rt△CFM和Rt△BEM中,根据斜边相等,由勾股定理列方程求b,再将M点坐标代入反比例函数式即可.
| 1 |
| 2 |
解答: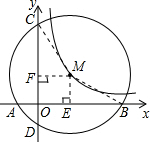 解:过点M作ME⊥x轴,MF⊥y轴,垂足为E、F,连接MB、MC,
解:过点M作ME⊥x轴,MF⊥y轴,垂足为E、F,连接MB、MC,
由垂径定理可知BE=
AB=4,
∴OE=MF=OB-BE=2,
OF=ME=b,则FC=4-b,
在Rt△CFM和Rt△BEM中,
CF2+FM2=CM2=BM2=EM2+BE2,
即(4-b)2+22=b2+42,
解得b=
,
∴M(2,
),将点M坐标代入反比例函数式y=
,
得k=xy=1,
∴y=
.
故本题答案为:y=
.
 解:过点M作ME⊥x轴,MF⊥y轴,垂足为E、F,连接MB、MC,
解:过点M作ME⊥x轴,MF⊥y轴,垂足为E、F,连接MB、MC,由垂径定理可知BE=
| 1 |
| 2 |
∴OE=MF=OB-BE=2,
OF=ME=b,则FC=4-b,
在Rt△CFM和Rt△BEM中,
CF2+FM2=CM2=BM2=EM2+BE2,
即(4-b)2+22=b2+42,
解得b=
| 1 |
| 2 |
∴M(2,
| 1 |
| 2 |
| k |
| x |
得k=xy=1,
∴y=
| 1 |
| x |
故本题答案为:y=
| 1 |
| x |
点评:此题主要考查反比例函数解析式的求法,注意通过解方程求出M点坐标,同时要注意运用数形结合的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
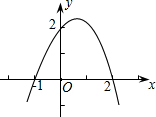 如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当y>2时,自变量x的取值范围是( )
如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当y>2时,自变量x的取值范围是( )A、0<x<
| ||
| B、0<x<1 | ||
C、
| ||
| D、-1<x<2 |
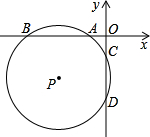 如图,⊙P与两坐标轴分别交于点A(-2、0)、B(-6、0)、C(0、-3)和点D,双曲线
如图,⊙P与两坐标轴分别交于点A(-2、0)、B(-6、0)、C(0、-3)和点D,双曲线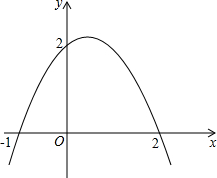 (2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),
(2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2), 如图:一次函数与两坐标轴交于A,B两点,与反比例函数交于C,D两点,已知点A(2,0)且OA=OB=AC=BD,求一次函数与反比例函数的解析式.
如图:一次函数与两坐标轴交于A,B两点,与反比例函数交于C,D两点,已知点A(2,0)且OA=OB=AC=BD,求一次函数与反比例函数的解析式.