题目内容
 如图:一次函数与两坐标轴交于A,B两点,与反比例函数交于C,D两点,已知点A(2,0)且OA=OB=AC=BD,求一次函数与反比例函数的解析式.
如图:一次函数与两坐标轴交于A,B两点,与反比例函数交于C,D两点,已知点A(2,0)且OA=OB=AC=BD,求一次函数与反比例函数的解析式.分析:作CF⊥x轴于F点,由点A(2,0)且OA=OB=AC=BD,则B点坐标为(0,-2),△OAB为等腰直角三角形,AC=2,易得△ACF为等腰直角三角形,于是AF=CF=
AC=
,可确定C点坐标为(2+
,
),然后用待定系数法确定两函数的解析式.
| ||
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:作CF⊥x轴于F点,如图,
∵点A(2,0)且OA=OB=AC=BD,
∴B点坐标为(0,-2),△OAB为等腰直角三角形,AC=2,
∴∠OAB=45°,
∴∠CAF=45°,
∴△ACF为等腰直角三角形,
∴AF=CF=
AC=
,
∴C点坐标为(2+
,
),
设反比例函数的解析式为y=
(k≠0),
把C(2+
,
)代入得k=
(2+
)=2
+2,
∴反比例函数的解析式为y=
.
设一次函数的解析式为y=ax+b,
把A(2,0)),B(0,-2)代入得
,解得
,
∴一次函数的解析式为y=x-2.

∵点A(2,0)且OA=OB=AC=BD,
∴B点坐标为(0,-2),△OAB为等腰直角三角形,AC=2,
∴∠OAB=45°,
∴∠CAF=45°,
∴△ACF为等腰直角三角形,
∴AF=CF=
| ||
| 2 |
| 2 |
∴C点坐标为(2+
| 2 |
| 2 |
设反比例函数的解析式为y=
| k |
| x |
把C(2+
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴反比例函数的解析式为y=
2
| ||
| x |
设一次函数的解析式为y=ax+b,
把A(2,0)),B(0,-2)代入得
|
|
∴一次函数的解析式为y=x-2.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式.

练习册系列答案
相关题目
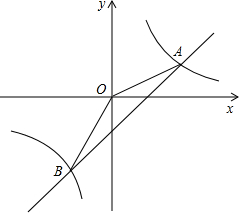 图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA=
图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA= 的
的 图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA=
图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA=
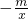 =0的解(直接写出答案);
=0的解(直接写出答案);