题目内容
12. 如图,直线y=-2x+4与x轴交于点A,与y轴交于点B,抛物线y=-2x2+bx+c经过A、B两点.
如图,直线y=-2x+4与x轴交于点A,与y轴交于点B,抛物线y=-2x2+bx+c经过A、B两点.(1)求抛物线的解析式;
(2)P为直线AB上的动点,当点P绕原点O旋转180°的对应点Q在抛物线上时,求点P的坐标;
(3)M为直线AB上的动点,N为抛物线上的动点,当以点O,A,M,N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
分析 (1)首先求出A、B两点坐标,然后把A、B两点坐标代入抛物线解析式即可解决问题.
(2)设P(m,-2m+4)则Q(-m,2m-4),把点Q坐标代入y=-2x2+2x+4中,解方程即可解决问题.
(3)分两种情形讨论①当OA为平行四边形OAMN的边时,MN=0A=2,则N(m-2,-2m+4),把点N坐标代入y=-2x2+2x+4中,解方程即可.②当OA为对角线时,
因为OA与MN互相平分,OA的中点(1,0),推出N(2-m,2m-4),把N点坐标代入y=-2x2+2x+4解方程即可.
解答 解:(1)∵直线y=-2x+4与x轴交于点A,与y轴交于点B,
∴A(2,0),B(0,4),
把A、B两点坐标代入y=-2x2+bx+c,
得到$\left\{\begin{array}{l}{c=4}\\{-8+2b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=2}\\{c=4}\end{array}\right.$,
∴抛物线的解析式为y=-2x2+2x+4.
(2)设P(m,-2m+4)则Q(-m,2m-4),
把点Q坐标代入y=-2x2+2x+4中,
得2m-4=-2m2-2m+4,
解得m=-1$±\sqrt{5}$,
∴点P坐标为(-1+$\sqrt{5}$,6-2$\sqrt{5}$)或(-1-$\sqrt{5}$,6+2$\sqrt{5}$).
(3)设M(m,-2m+4),由题意A(2,0),
①当OA为平行四边形OAMN的边时,MN=0A=2,则N(m-2,-2m+4),
把点N坐标代入y=-2x2+2x+4中,
得-2m+4=-2(m-2)2+2(m-2)=4,
整理得m2-6m+6=0,
解得m=3±$\sqrt{3}$,
∴点M坐标为(3+$\sqrt{3}$,-2-2$\sqrt{3}$)或(3-$\sqrt{3}$,-2+2$\sqrt{3}$).
②当OA为对角线时,
∵OA与MN互相平分,OA的中点(1,0),
∴N(2-m,2m-4),
把N点坐标代入y=-2x2+2x+4,
得到2m-4=-2(2-m)2=2(2-m)+4,
整理得m2-2m-2=0,
解得m=1$±\sqrt{3}$,
∴点M坐标为(1+$\sqrt{3}$,2-2$\sqrt{3}$)或(1-$\sqrt{3}$,2+2$\sqrt{3}$).
综上所述满足条件的点M坐标为(3+$\sqrt{3}$,-2-2$\sqrt{3}$)或(3-$\sqrt{3}$,-2+2$\sqrt{3}$)或(1+$\sqrt{3}$,2-2$\sqrt{3}$)或(1-$\sqrt{3}$,2+2$\sqrt{3}$).
点评 本题考查二次函数综合题、一次函数、待定系数法、平行四边形的性质、中点坐标公式等知识,解题的关键是灵活应用待定系数法解决问题,学会分类讨论,注意不能漏解,属于中考压轴题.

| A. | ①②③ | B. | ①②④ | C. | ④ | D. | ①② |
| A. | $\frac{{x}^{2}}{a}$ | B. | $\frac{a}{{x}^{2}}$ | C. | $\frac{{a}^{2}}{x}$ | D. | $\frac{x}{{a}^{2}}$ |
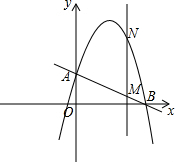 如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.
如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.