题目内容
5.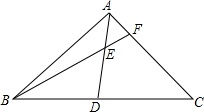 如图,在△ABC中,D是BC边的中点,E是AD上一点,BE=AC,BE的延长线交AC于F,求证:∠AEF=∠EAF.
如图,在△ABC中,D是BC边的中点,E是AD上一点,BE=AC,BE的延长线交AC于F,求证:∠AEF=∠EAF.
分析 延长AD到G使DG=AD,连接BG,通过△ACD≌△GBD,根据全等三角形的性质得到∠CAD=∠G,AC=BG,等量代换得到BE=BG,由等腰三角形的性质得到∠G=∠BEG,即可得到结论.
解答 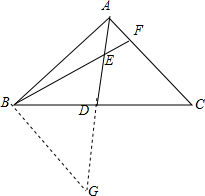 解:如图,延长AD到G使DG=AD,连接BG,
解:如图,延长AD到G使DG=AD,连接BG,
在△ACD与△GBD中,
$\left\{\begin{array}{l}{CD=BD}\\{∠ADC=∠BDG}\\{AD=DG}\end{array}\right.$,
∴△ACD≌△GBD,
∴∠CAD=∠G,AC=BG,
∵BE=AC,
∴BE=BG,
∴∠G=∠BEG,
∵∠BEG=∠AEF,
∴∠AEF=∠EAF.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
15.如果3x2n-1ym与x3y3是同类项,则m,n值( )
| A. | 3和-2 | B. | -3和-2 | C. | 3和2 | D. | -3和-2 |
 用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,用101根火柴棒可以摆出20个六边形.
用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,用101根火柴棒可以摆出20个六边形.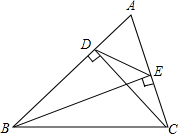 如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.
如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.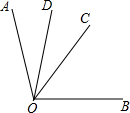 如图,0C是∠A0B的平分线,OD是∠AOC的平分线,且∠BOC+∠COD=75°,求∠BOC和∠COD的度数各是多少度?
如图,0C是∠A0B的平分线,OD是∠AOC的平分线,且∠BOC+∠COD=75°,求∠BOC和∠COD的度数各是多少度? 已知:∠A+∠C=∠B=60°,AD=CE,求证:BE=CD.
已知:∠A+∠C=∠B=60°,AD=CE,求证:BE=CD.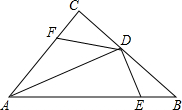 如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.
如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.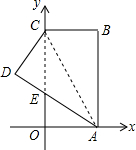 如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(4,8),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为(-$\frac{12}{5}$,$\frac{24}{5}$).
如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(4,8),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为(-$\frac{12}{5}$,$\frac{24}{5}$).