题目内容
14．
货车和轿车同时从A地沿笔直的公路去B地，轿车到B地停留一段时间后，原路原速返回，两辆车相遇前，它们之间的距离y（km）与它们离开A地的时间t（h）之间的函数关系如图所示，则两车相遇时的时间为（ ）| A． | 3.25h | B． | 3.50h | C． | 3.75h | D． | 4h |
分析 根据题意和函数图象中的数据可以求得A车和B车的速度，从而可以求得当两车相遇时的方程，从而可以求得相遇时的时间．
解答 解：由题意可得，
A车的速度为：（120-90）÷（3-2）=30km/h，
B车的速度为：$\frac{120+30×2}{2}$=90km/h，
设两车相遇的时间为xh，
30x+90（x-1）=90×2×2，
解得，x=3.75，
故选C．
点评 本题考查一次函数的应用、一元一次方程的应用，解答本题的关键是明确题意，求出两车的速度，写出两车相遇时的方程，利用数形结合的思想解答．
练习册系列答案
相关题目
4．
如图是某游乐城的平面示意图，如图用（8，2）表示入口处的位置，用（6，-1）表示球幕电影的位置，那么坐标原点表示的位置是（ ）
如图是某游乐城的平面示意图，如图用（8，2）表示入口处的位置，用（6，-1）表示球幕电影的位置，那么坐标原点表示的位置是（ ）| A． | 太空秋千 | B． | 梦幻艺馆 | C． | 海底世界 | D． | 激光战车 |
2．甲、乙、丙三名射箭运动员在某次测试中各射箭8次，三人的测试成绩如表：
s2甲、s2乙、s2丙分别表示甲、乙、丙三名运动员这次测试成绩的方差，下面各式中正确的是（ ）
| 甲的成绩 | 乙的成绩 | 丙的成绩 | ||||||||||||||
| 环数 | 7 | 8 | 9 | 10 | 环数 | 7 | 8 | 9 | 10 | 环数 | 7 | 8 | 9 | 10 | ||
| 频数 | 1 | 3 | 3 | 1 | 频数 | 2 | 2 | 2 | 2 | 频数 | 3 | 1 | 1 | 3 | ||
| A． | s2甲＞s2乙＞s2丙 | B． | s2乙＞s2甲＞s2丙 | C． | s2丙＞s2甲＞s2乙 | D． | s2丙＞s2乙＞s2甲 |
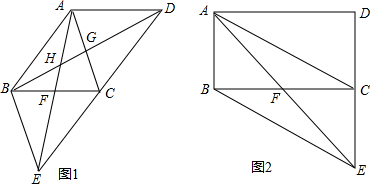
如图，点B是扇形AOC的弧AC的二等分点，过点B、C分别作半径的垂线段BD、CE，垂足分别为D、E，已知OA⊥OC，半径OC=1，则图中阴影部分的面积和是$\frac{π}{4}$-$\frac{1}{2}$．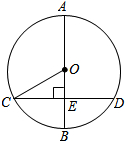
如图，AB是⊙O的直径，弦CD⊥AB于点E，连结CO．如果CO=2cm，∠COE=60°，那么劣弧$\widehat{CD}$的长是$\frac{4}{3}$πcm．