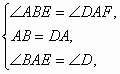Question

如图(1)，在正方形ABCD中，E，F分别是边AD、DC上的点，且AF⊥BE． (1)求证：AF＝BE． (2)如图(2)，在正方形ABCD中，M、N、P、Q分别是边AB、BC、CD、DA上的点，且MP⊥NQ．MP与NQ是否相等？请说明理由．

Answer 1

答案：
解析：

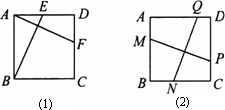
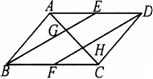
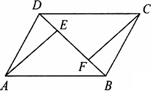
(1)证明：在正方形ABCD中，AB＝AD，∠BAE＝∠D＝90°， 　　∴∠DAF＋∠BAF＝90°， 　　∵AF⊥BE， 　　∴∠ABE＋∠BAF＝90°， 　　∴∠ABE＝∠DAF． 　　在△ABE和△DAF中， 　　 　　∴△ABE≌△DAF， 　　∴AF＝BE． 　　(2)解：MP与NQ相等． 　　理由如下：过点A作AF∥MP交CD于F，过点B作BE∥NQ交AD于E， 　　则AF＝MP，BE＝NQ． 　　同(1)可证△AFD≌△BEA， 　　∴AF＝BE， 　　∴MP＝NQ．