题目内容
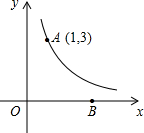 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.
考点:待定系数法求反比例函数解析式,待定系数法求一次函数解析式
专题:数形结合,待定系数法
分析:(1)利用待定系数法把A(1,3)代入反比例函数y=
可得k的值,进而得到解析式;
(2)根据△AOB的面积为6求出B点坐标,再设直线AB的解析式为y=kx+b,把A、B两点代入可得k、b的值,进而得到答案.
| k |
| x |
(2)根据△AOB的面积为6求出B点坐标,再设直线AB的解析式为y=kx+b,把A、B两点代入可得k、b的值,进而得到答案.
解答:解:(1)∵反比例函数y=
(k为常数,且k≠0)经过点A(1,3),
∴3=
,
解得:k=3,
∴反比例函数解析式为y=
;
(2)设B(a,0),则BO=a,
∵△AOB的面积为6,
∴
•a•3=6,
解得:a=4,
∴B(4,0),
设直线AB的解析式为y=kx+b,
∵经过A(1,3),B(4,0),
∴
,
解得
,
∴直线AB的解析式为y=-x+4.
| k |
| x |
∴3=
| k |
| 1 |
解得:k=3,
∴反比例函数解析式为y=
| 3 |
| x |
(2)设B(a,0),则BO=a,
∵△AOB的面积为6,
∴
| 1 |
| 2 |
解得:a=4,
∴B(4,0),
设直线AB的解析式为y=kx+b,
∵经过A(1,3),B(4,0),
∴
|
解得
|
∴直线AB的解析式为y=-x+4.
点评:此题主要考查了待定系数法求一次函数解析式和反比例函数解析式,关键是正确求出B点坐标.

练习册系列答案
相关题目
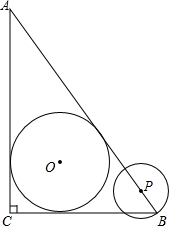 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.
如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.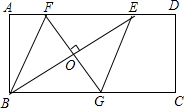 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE= 如图,?ABCD的对角线AC、BD相交于点O,EF过点O且与AB,CD分别相交于点E、F,求证:△AOE≌△COF.
如图,?ABCD的对角线AC、BD相交于点O,EF过点O且与AB,CD分别相交于点E、F,求证:△AOE≌△COF.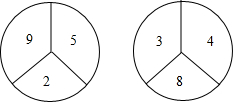 有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定,转动两个转盘各一次,指向大的数字获胜.现由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?
有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定,转动两个转盘各一次,指向大的数字获胜.现由你和小明各选择一个转盘游戏,你会选择哪一个,为什么? 如图,已知点A、B、C在⊙O上,CD⊥OB于D,AB=2OD,若∠C=40°,则∠B=
如图,已知点A、B、C在⊙O上,CD⊥OB于D,AB=2OD,若∠C=40°,则∠B=