题目内容
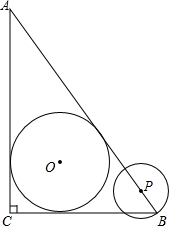 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.
如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.(1)求⊙O的半径;
(2)点P从点B沿边BA向点A以1cm/s的速度匀速运动,以P为圆心,PB长为半径作圆,设点P运动的时间为t s,若⊙P与⊙O相切,求t的值.
考点:圆的综合题
专题:几何图形问题,压轴题,动点型
分析:(1)求圆的半径,因为相切,我们通常连接切点和圆心,设出半径,再利用圆的性质和直角三角形性质表示其中关系,得到方程,求解即得半径.
(2)考虑两圆相切,且一圆已固定,一般就有两种情形,外切与内切.所以我们要分别讨论,当外切时,圆心距等于两圆半径的和;当内切时,圆心距等于大圆与小圆半径的差.分别作垂线构造直角三角形,类似(1)通过表示边长之间的关系列方程,易得t的值.
(2)考虑两圆相切,且一圆已固定,一般就有两种情形,外切与内切.所以我们要分别讨论,当外切时,圆心距等于两圆半径的和;当内切时,圆心距等于大圆与小圆半径的差.分别作垂线构造直角三角形,类似(1)通过表示边长之间的关系列方程,易得t的值.
解答:解:(1)如图1,设⊙O与AB、BC、CA的切点分别为D、E、F,连接OD、OE、OF,

则AD=AF,BD=BE,CE=CF.
∵⊙O为△ABC的内切圆,
∴OF⊥AC,OE⊥BC,即∠OFC=∠OEC=90°.
∵∠C=90°,
∴四边形CEOF是矩形,
∵OE=OF,
∴四边形CEOF是正方形.
设⊙O的半径为rcm,则FC=EC=OE=rcm,
在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,
∴AB=
=5cm.
∵AD=AF=AC-FC=4-r,BD=BE=BC-EC=3-r,
∴4-r+3-r=5,
解得 r=1,即⊙O的半径为1cm.
(2)如图2,过点P作PG⊥BC,垂足为G.

∵∠PGB=∠C=90°,
∴PG∥AC.
∴△PBG∽△ABC,
∴
=
=
.
∵BP=t,
∴PG=
×BP=
t,BG=
×BP=
t.
若⊙P与⊙O相切,则可分为两种情况,⊙P与⊙O外切,⊙P与⊙O内切.
①当⊙P与⊙O外切时,

如图3,连接OP,则OP=1+t,过点P作PH⊥OE,垂足为H.
∵∠PHE=∠HEG=∠PGE=90°,
∴四边形PHEG是矩形,
∴HE=PG,PH=GE,
∴OH=OE-HE=1-
t,PH=GE=BC-EC-BG=3-1-
t=2-
t.
在Rt△OPH中,
由勾股定理,(1-
t)2+(2-
t)2=(1+t)2,
解得 t=
.
②当⊙P与⊙O内切时,

如图4,连接OP,则OP=t-1,过点O作OM⊥PG,垂足为M.
∵∠MGE=∠OEG=∠OMG=90°,
∴四边形OEGM是矩形,
∴MG=OE,OM=EG,
∴PM=PG-MG=
t-1,
OM=EG=BC-EC-BG=3-1-
t=2-
t,
在Rt△OPM中,
由勾股定理,(
t-1)2+(2-
t)2=(t-1)2,
解得 t=2.
综上所述,⊙P与⊙O相切时,t=
s或t=2s.

则AD=AF,BD=BE,CE=CF.
∵⊙O为△ABC的内切圆,
∴OF⊥AC,OE⊥BC,即∠OFC=∠OEC=90°.
∵∠C=90°,
∴四边形CEOF是矩形,
∵OE=OF,
∴四边形CEOF是正方形.
设⊙O的半径为rcm,则FC=EC=OE=rcm,
在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,
∴AB=
| AC2+BC2 |
∵AD=AF=AC-FC=4-r,BD=BE=BC-EC=3-r,
∴4-r+3-r=5,
解得 r=1,即⊙O的半径为1cm.
(2)如图2,过点P作PG⊥BC,垂足为G.

∵∠PGB=∠C=90°,
∴PG∥AC.
∴△PBG∽△ABC,
∴
| PG |
| AC |
| BG |
| BC |
| BP |
| BA |
∵BP=t,
∴PG=
| AC |
| BA |
| 4 |
| 5 |
| BC |
| BA |
| 3 |
| 5 |
若⊙P与⊙O相切,则可分为两种情况,⊙P与⊙O外切,⊙P与⊙O内切.
①当⊙P与⊙O外切时,

如图3,连接OP,则OP=1+t,过点P作PH⊥OE,垂足为H.
∵∠PHE=∠HEG=∠PGE=90°,
∴四边形PHEG是矩形,
∴HE=PG,PH=GE,
∴OH=OE-HE=1-
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
在Rt△OPH中,
由勾股定理,(1-
| 4 |
| 5 |
| 3 |
| 5 |
解得 t=
| 2 |
| 3 |
②当⊙P与⊙O内切时,

如图4,连接OP,则OP=t-1,过点O作OM⊥PG,垂足为M.
∵∠MGE=∠OEG=∠OMG=90°,
∴四边形OEGM是矩形,
∴MG=OE,OM=EG,
∴PM=PG-MG=
| 4 |
| 5 |
OM=EG=BC-EC-BG=3-1-
| 3 |
| 5 |
| 3 |
| 5 |
在Rt△OPM中,
由勾股定理,(
| 4 |
| 5 |
| 3 |
| 5 |
解得 t=2.
综上所述,⊙P与⊙O相切时,t=
| 2 |
| 3 |
点评:本题考查了圆的性质、两圆相切及通过设边长,表示其他边长关系再利用直角三角形求解等常规考查点,总体题目难度不高,是一道非常值得练习的题目.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列说法中错误的是( )
| A、掷一枚均匀的骰子,骰子停止转动后6点朝上是必然事件 | ||||
| B、了解一批电视机的使用寿命,适合用抽样调查的方式 | ||||
| C、若a为实数,则|a|<0是不可能事件 | ||||
D、甲、乙两人各进行10次射击,两人射击成绩的方差分别为
|
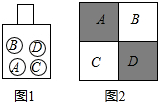 如图1,在一个不透明的袋中装有四个球,分别标有字母A、B、C、D,这些球除了所标字母外都相同,另外,有一面白色、另一面黑色、大小相同的4张正方形卡片,每张卡片上面的字母相同,分别标有A、B、C、D.最初,摆成图2的样子,A、D是黑色,B、C是白色.
如图1,在一个不透明的袋中装有四个球,分别标有字母A、B、C、D,这些球除了所标字母外都相同,另外,有一面白色、另一面黑色、大小相同的4张正方形卡片,每张卡片上面的字母相同,分别标有A、B、C、D.最初,摆成图2的样子,A、D是黑色,B、C是白色. )
) 如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,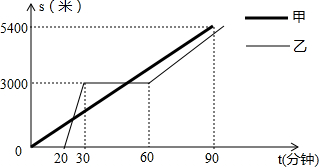 某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据以上信息回答下列问题:
某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据以上信息回答下列问题: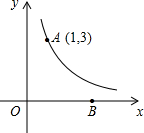 如图,反比例函数y=
如图,反比例函数y= 小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是
小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是