��Ŀ����
��֪�����߾�������A(2,6)��B(-1,0)��C(3,0)��
����������������Ӧ�Ķ��κ����Ľ���ʽ��
��2��д�����ĶԳ���Ͷ�������.
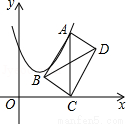
��1��y=-2x²+4x+6����2���Գ���Ϊx=1����������Ϊ��1��8�� �������������������1����Ŀ��֪��������x��Ľ������꣬�ʽ���������ʽ��Ϊ����ʽ���ٽ���һ�����������뺯������ʽ�������ʽ�е�δ֪�������ɣ���2������������ʽ��Ϊ����ʽ��д���Գ���Ͷ�������. ��������� �������� ��1����y=a��x+1����x��3���� ��A(2��6)�������ʽ����6=a��2+1��...��ͼ����ƽ��ֱ������ϵ�У���A��������y=x2��2x+4���˶�������A��AC��x���ڵ�C����ACΪ�Խ���������ABCD������BD����Խ���BD����СֵΪ____��
��ͼ���ڡ�ABC�У�BC��4���Ե�AΪԲ�ģ�2Ϊ�뾶�ġ�A��BC�����ڵ�D����AB��E����AC��F����P�ǡ�A�ϵ�һ�㣬�ҡ�EPF��40�㣬��ͼ����Ӱ���ֵ������__________���������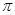 ��
��
��ͼ������������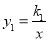 ������������y2=k2x ��ͼ����A��-1��-3����B��1��3�����㣬��
������������y2=k2x ��ͼ����A��-1��-3����B��1��3�����㣬��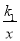 ��k2x����x��ȡֵ��Χ��___________________.
��k2x����x��ȡֵ��Χ��___________________.
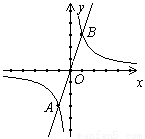
��֪��A(��1��y1)��B(2��y2)����˫����y�� �ϣ���y1��y2����m��ȡֵ��Χ��______________
�ϣ���y1��y2����m��ȡֵ��Χ��______________
��������y��x2��2x��3��x��ֱ���A��B���㣬��AB�ij�Ϊ ______��
�鿴�� ��������- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д���֪����x2+mx��3=0��һ������1����������һ������______��
-3 ������������һ��Ϊ����1��= -3 �� ��ã� =��3�� �ʴ�Ϊ����3����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣���Գ���Ϊx=��1���ҹ��㣨��3��0��������˵����
��abc��0��
��2a��b=0��
��4a+2b+c��0��
��������5��y1������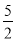 ��y2���������������㣬��y1��y2��
��y2���������������㣬��y1��y2��
����˵����ȷ���ǣ�������
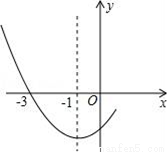
A. �٢� B. �ڢ� C. �٢ڢ� D. �ڢۢ�
�鿴����ͼ��ij����һ�ǣ���AOB=90�㣬��AB�İ뾶OA����6�ף�C��OA���е㣬��D�ڻ�AB�ϣ�CD��OB����ͼ������������Ӱ���֣�������ǣ�������
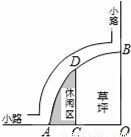
A. ��10��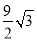 ����2 B. ����
����2 B. ����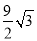 ����2 C. ��6��
����2 C. ��6��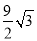 ����2 D. ��6��
����2 D. ��6�� ����2
����2
����һ��Բ�Ľ�Ϊ108�㣬�뾶Ϊ40cm������ֽƬ��С���ȥԲ�Ľ�Ϊ�ȵIJ�������ֽƬ��ʣ�µ�ֽƬ������һ������뾶Ϊ10cm��Բ��ֽñ���ӷ촦���ص��������ȥ������ֽƬ��Բ�ĽǦ�Ϊ���� ��
A. 18 B. 30 C. 45 D . 60
�鿴������ͼ4��4��������������,��MNP��ij����תһ���ĽǶ�,�õ���M1N1P1,������ת���Ŀ�����(����)
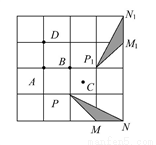
A. ��A B. ��B C. ��C D. ��D
�鿴����һ�������ĺ�������20������ɫ�����ͬ��С��ÿ������ǰ�Ƚ����е���ҡ�ȣ��������һ���������ɫ���ٷŻغ��У�ͨ�������ظ���������������������Ƶ���ȶ���0.3���ɴ˿ɹ��ƺ��к���ĸ���ԼΪ��������
A. 3 B. 6 C. 7 D. 14
�鿴�� ��������- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
ˮ�����Ű�����ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�Ϊ��֤ÿ�������۳�260��Ű��̾����������ۣ�
(1)��������ˮ��ÿ����ۼ۽���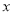 Ԫ����ÿ�����������__________��(�ú�
Ԫ����ÿ�����������__________��(�ú�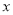 �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
(2)��������ˮ��Ҫ��ÿ��ӯ��300Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
��1����100��200������2���Ű����轫ÿ����ۼ۽���1Ԫ. �����������������(1)������Ŀ�н��۶����������Ĺ�ϵ��ʽ.(2)���յ���������һԪ���η��̽�Ӧ����. ��������� ��1����100��200���� ��2��������ɵã� �� �����ɵã� ��������̵ã� �� ��ʱ��100��200��100��200��1 ��300��260 �� ��ʱ��100��200��100...��ͼ�����ı���ABCD�У���A����BCD��90�㣬BC��DC���ӳ�AD��E��ʹDE��AB.
��1����֤����ABC����EDC��
��2����֤����ABC�ա�EDC.
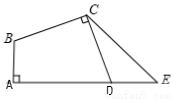
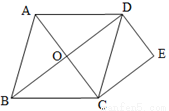
��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O������C��CE��BD������D��DE��AC��CE��DE�ཻ�ڵ�E��
��1����֤���ı���CODE�Ǿ��Σ�
��2����AB=5��AC=6�����ı���CODE���ܳ���
��ͼ����·���£�С����������ͼ���߶�AB��ʾ�����ڵ����ϵ�Ӱ����ͼ���߶�AC��ʾ��С����������ͼ���߶�FG��ʾ��·�Ƶ������߶�DE�ϣ�
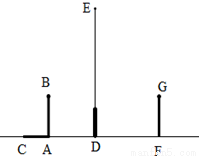
��1������ȷ���������ڵ�λ�ã�������С���ڵƹ����γɵ�Ӱ�ӣ�
��2�����С��������AB=1.6m������Ӱ�ӳ�AC=1.4m��������·�Ƶľ���AD=2.1m������ݵĸ�.
�鿴����һ�����Ѿ۲��У���A��B��C��D�����ز˿ɹ�ѡ��С������ѡ��һ�֣�С��Ҳ����ѡ��һ�֣���С��ѡ��IJ���ͬ�����������б�����״ͼ�ķ������A��B�����ز˱�ѡ�еĸ��ʣ�
�鿴��ֱ��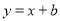 �뷴��������
�뷴��������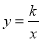 ��
��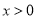 ����ͼ���ڵ�A��1��2�����������������ı���ʽ.
����ͼ���ڵ�A��1��2�����������������ı���ʽ.
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�����ж���ȷ���ǣ�������
A. ��AB��BC���� ABCD������ B. ��AC��BD����
ABCD������ B. ��AC��BD���� ABCD��������
ABCD��������
C. ��AC=BD����  ABCD�Ǿ��� D. ��AB=AD����
ABCD�Ǿ��� D. ��AB=AD���� ABCD��������
ABCD��������
��ͼ��ͬһʱ��ѧУ��һ��������˵�Ӱ�ӣ��������Ϊ3�ף��������Ӱ�ӳ�Ϊ1.2�ף���˵ĸ߶�Ϊ5�ף�������Ӱ�ӳ�Ϊ�� ��
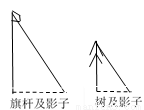
A. 4�� B. 2�� C. 1.8�� D. 3.6��
�鿴������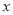 ��һԪ���η���
��һԪ���η���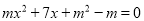 �ij�����Ϊ0����
�ij�����Ϊ0����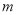 ��ֵ���ڣ� ��
��ֵ���ڣ� ��
A. 1 B. 2 C. 0��1 D. 0
�鿴�����и����߶�(��λ��cm)�У��ɱ����߶ε��� (�� ��)
A. 1��2��3��4 B. 1��2��2��4 C. 3��5��9��13 D. 1��2��2��3
�鿴����������ͬ���ƣ�ÿ�������Ҵ�С��ͬ�������Ƶ��������ֱַ���0��1����ÿ�����и�����һ���ƣ������Ƶ��������ֺ�Ϊ1�ĸ���Ϊ�� ��
A. 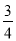 B.
B. 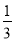 C.
C. 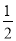 D.
D. 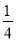
��P����2�� 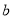 ���Ƿ���������
���Ƿ���������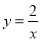 ��ͼ���ϵ�һ�㣬��
��ͼ���ϵ�һ�㣬��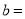 �� ��
�� ��
A. 2 B. 1 C. -2 D. -1
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
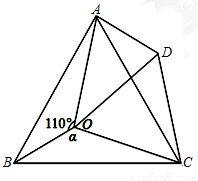
��ͼ����O�ǵȱߡ�ABC��һ�㣬��AOB=110�㣬��BOC=��������BOC�Ƶ�C��˳ʱ�뷽����ת60��á�ADC������OD��
��1����֤����COD�ǵȱ������Σ�
��2������=150��ʱ�����жϡ�AOD����״����˵�����ɣ�
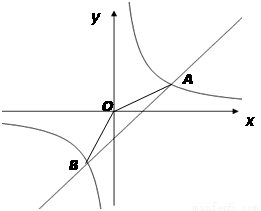
һ�κ���y=kx+b��ͼ���뷴��������y=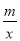 ��ͼ���ڵ�A��2��1����B����1��n������.
��ͼ���ڵ�A��2��1����B����1��n������.
��1�����������Ľ���ʽ��
��2����һ���������Ľ���ʽ��
��3�����AOB�����.
��ͼ��ʾ�� ��һ�������ش�10m �ߵĴ�A����ˮ��������ˮ�������ˮ��������״����������ߵ���ߵ�M ��ǽ1m�������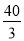 m.
m.
��1���������ߵĽ���ʽ��
��2����ˮ����ص�B��ǽ�ľ���OB.
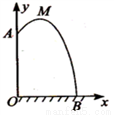
��ͼ��ʾ��AB�ǡ�O��ֱ����BD�ǡ�O���ң��ӳ�BD����C��ʹDC=BD������AC������D��DE��AC��E��
��1����֤��AB=AC��
��2����֤��DEΪ��O�����ߣ�
�̵�ֻ��ѩ�̡����֡���֭����֭�������ϣ�ÿ�������������㣬ijͬѧȥ�õ깺�����ϣ�ÿ�����ϱ�ѡ�еĿ�������ͬ��
��1������ȥ��һƿ���ϣ���������֭�ĸ����� ��
��2����������ȥ�����ϣ�ÿ����һƿ����������������Ʒ�ֲ�ͬ��������״ͼ���б��������ǡ����ѩ�̺���֭�ĸ��ʣ�
�鿴����֪�����߾�������A(2,6)��B(-1,0)��C(3,0)��
����������������Ӧ�Ķ��κ����Ľ���ʽ��
��2��д�����ĶԳ���Ͷ�������.
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��������y��x2��2x��3��x��ֱ���A��B���㣬��AB�ij�Ϊ ______��
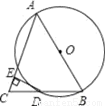
4 ����������������κ�����x���2���������꣬Ȼ�������2��֮��ľ��룮 �������� ���κ���y=x2-2x-3��x�ύ��A��B�ĺ�����ΪһԪ���η���x2-2x-3=0�������������x1=-1��x2=3����AB=|x2-x1|=4��ֱ��y=x+3����һ��P(3,a)�����P����ԭ��ĶԳƵ�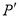 Ϊ___________.
Ϊ___________.
��ͼ����������������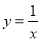 ��
��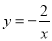 ��ͼ��ֱ���l1��l2�����P��l1�ϣ�PC��x�ᣬ����ΪC����l2�ڵ�A��PD��y�ᣬ����ΪD����l2�ڵ�B�����PAB�����Ϊ��������
��ͼ��ֱ���l1��l2�����P��l1�ϣ�PC��x�ᣬ����ΪC����l2�ڵ�A��PD��y�ᣬ����ΪD����l2�ڵ�B�����PAB�����Ϊ��������
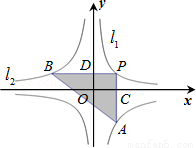
A. 3 B. 4 C. 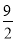 D. 5
D. 5
��ͼ�Ƕ��κ���y=ax2+bx+c��ͼ�����н��ۣ� �ٶ�������ʽax2+bx+c�����ֵΪ4��
��4a+2b+c��0��
��һԪ���η���ax2+bx+c=1������֮��Ϊ��1��
��ʹy��3������x��ȡֵ��Χ��x��0��
������ȷ�ĸ����У� ��
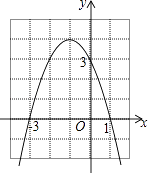
A. 1�� B. 2�� C. 3�� D. 4��
�鿴��ijͬѧ������㷨�����κ���y=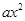 +bx+c��ͼ��ʱ���г�������ı���
+bx+c��ͼ��ʱ���г�������ı���
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | ��11 | ��2 | 1 | ��2 | ��5 | �� |
���ڴ��ģ������������һ��yֵ��������������ֵ�ǣ� ��.
A����11 B����2 C��1 D����5
�鿴����Բ�ĵ����Ϊ16��cm2��ĸ�߳�Ϊ12cm�������IJ���չ��ͼ��Բ�Ľ�Ϊ( )
A. 240�� B. 120�� C. 180�� D. 90��
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ��������ABCD�ڽ��ڡ�O����O��ֱ��Ϊ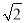 ���ף��������Բ����������һ�����ӣ���������������ABCD�ڵĸ����ǣ� ����
���ף��������Բ����������һ�����ӣ���������������ABCD�ڵĸ����ǣ� ����
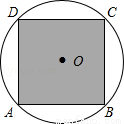
A��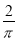 B��
B��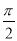 C��
C��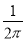 D��
D��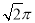
��ͼ��AB�ǡ�O��ֱ������CD��AB������ΪE�����AB=10��CD=8����ô�߶�OE�ij�Ϊ�� ��
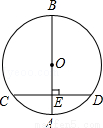
A��6 B��5 C��4 D��3
�鿴������������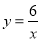 ͼ�����������㣨x1��y1������x2��y2������x3��y3��������x1��x2��0��x3����y1��y2��y3�Ĵ�С��ϵ��( )
ͼ�����������㣨x1��y1������x2��y2������x3��y3��������x1��x2��0��x3����y1��y2��y3�Ĵ�С��ϵ��( )
A. y2��y1��y3 B. y1��y2��y3 C. y3��y1��y2 D. y3��y2��y1
�鿴��һ��������װ�д�С����״��ͬ���ĸ������к���1��������1��������2����С������һ���Żأ�������һ���������ζ���������ĸ����ǣ� ��
A. 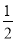 B.
B. 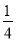 C.
C. 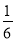 D.
D. 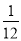
��ͼ����O�ǡ�ABC�����Բ����OCB��40�����A�Ķ�������( )
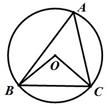
A. 60�� B. 50�� C. 40�� D. 30��
�鿴��������ͼ���У�������Գ�ͼ�Σ��������ĶԳ�ͼ�ε��ǣ� ��
A. 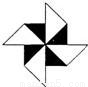 B .
B . C .
C . D.
D. 
- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
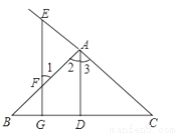
��ͼ��գ���֪��ͼ��AD��BC��D��EG��BC��G����E=��1��
��֤��ADƽ�֡�BAC��
֤������AD��BC��D��EG��BC��G�� ��֪ ��
���ADC=90�㣬��EGC=90�㣨___________��
���ADC=��EGC������������
��AD��EG��_____________��
���1=��2��___________��
��E=��3��___________��
�֡ߡ�E=��1�� ��֪��
���2=��3��___________��
��ADƽ�֡�BAC��___________����
Ϊ�˹���������������������������ȴ������д���30�������ϱ�ǣ�Ȼ��Ź�����������һ��ʱ�䣬���б�ǵ�����ȫ�������Ⱥ�У��ٴ���200���㣬�������д���ǵ�����5�����������й�����________���㣮
�鿴��һ�κ���y=��m2��4��x+��1��m����y=��m��1��x+m2��3��ͼ����y��ֱ��ڵ�P�͵�Q������P���Q����x��Գƣ���m=________
�鿴����ͼ���ڡ�ABC�У���BAC��90�㣬AB��AC����BAD��30�㣬AD��AE�����EDC�Ķ�����______��
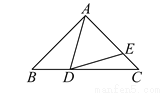
��ͼ����ABC�ա�DEF��A��D��B��E�ֱ��Ƕ�Ӧ���㣬��B=60�㣬��A=68�㣬AB=13cm�����F= ______�ȣ�DE= ____cm��
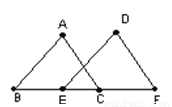
����ˬ��ͼ�����ĸ�ȫ�ȵ�ֱ�����������м�һ��С������ƴ�ɵĴ������Σ���ͼ����ֱ�������ε�����ֱ�DZߵij��ֱ���2��4����С��������������ε�������ǣ�������
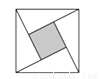
A. 1��2 B. 1��4 C. 1��5 D. 1��10
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
С����С�������ۡ����ʱΪʲôǹ����Ҫ�ǣ���
С��������������ֻ��һ��ֱ�ߣ�����ǹ����Ҫ���ǣ�
С�����������ۿ���һ�㣬�ǿ���һ�㣬Ŀ�꿴��һ�㣬�ⲻ�����������𣿶���һ����ѽ��
����˵˵��Ĺ۵㣮
����ȷ��һ��ֱ�� ������������������������ֱ�ߵ���������ȷ��һ��ֱ�߽��н�ɣ� ����������������ۿ���һ�㣬�ǿ���һ�㣬Ŀ�꿴��һ�㣬��ôҪ������Ŀ�꣬������Ŀ��ȷ��������ֱ�ߣ�Ӧ���ӵ����ߵ�ֱ���غϣ������Ǻ�Ŀ����ȷ��������ֱ���غϣ����ﵽ�����Ĵ��Ķ��� ���仰˵Ҫ������Ŀ��ͱ���ʹ����������Ŀ����ȷ����ֱ���ϣ���������ԲȦ�ֱ��ʾ�������Ϻ��������ϣ�����������ԲȦ�ڸ����������������������������ڸ��������ڣ��������������ڣ���������Ӧ�����������˵��������ԲȦ���ص����ֱ�ʾʲô���ļ�����

��֪x+12ƽ�����ǡ�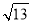 ��2x+y��6����������2����3xy������ƽ������
��2x+y��6����������2����3xy������ƽ������
��֪��|a��1|+|b+2|=0����2a+b��ֵ��
�鿴����ͼ��һ�����������ĵ���߳�Ϊ2cm����Ϊ4cm��
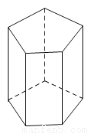
��1������������ж��ٸ��棿�������IJ������
��2������������ж��ٸ����㣿�ж������⣿
��3�����ú���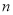 �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ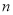 �����Ķ������������������������
�����Ķ������������������������
�ڵ�ʽ������������ǡ�����x2��y2+8y��4=x2����___________����
�鿴�� ��������- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������

