题目内容
10．
在平面直角坐标系中，画出函数y=-3x2+6x+1的图象，并求出它的最值．
分析 确定的顶点坐标和对称轴及与坐标轴的交点坐标即可作出其图象．
解答 解：∵y=-3x2+6x+1=-3（x-1）2+4，
∴二次函数的顶点坐标为（1，4），故其最大值为：4，
令y=-3x2+6x+1=0，
解得：x=1+$\frac{2\sqrt{3}}{3}$或x=1-$\frac{2\sqrt{3}}{3}$，
故抛物线与x轴交于（1+$\frac{2\sqrt{3}}{3}$，0）和（1-$\frac{2\sqrt{3}}{3}$，0），
故图象为：
．
点评 本题考查了二次函数的性质与图象，解题的关键是确定二次函数的顶点坐标及对称轴．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图所示，M、N分别是AB、CD的中点，MN=a，BC=b，求AD的长．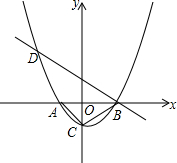
如图，已知抛物线y=m（x+1）（x-2）（m为常数，且m＞0）与x轴从左至右依次交于A、B两点，与y轴交于点C，且OA=OC，经过点B的直线与抛物线的另一交点D在第二象限．