题目内容
2.把抛物线y=-x2向上平移4个单位,再向左平移一个单位.那么所得的抛物线与x轴的两个交点之间的距离是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 先由平移规律求出新抛物线的解析式,然后求出抛物线与x轴的两个交点横坐标,利用坐标轴上两点间距离公式即可求得距离.
解答 解:所得抛物线为y=-(x+1)2+4,当y=0时,-(x+1)2+4=0,解得x1=1,x2=-3,
∴两个交点之间的距离是|-3-1|=4.
故选B.
点评 主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.

练习册系列答案
相关题目
7.方程(x-2)(x-3)=0的解是( )
| A. | 3 | B. | 2 | C. | 3和2 | D. | 0 |
 在平面直角坐标系中,画出函数y=-3x2+6x+1的图象,并求出它的最值.
在平面直角坐标系中,画出函数y=-3x2+6x+1的图象,并求出它的最值.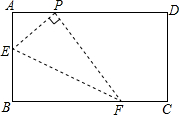 如图,在矩形ABCD中,点P在AD上,AB=2,AP=1,E是AB上的一个动点,连接PE,过点P作PE的垂线,交BC于点F,连接EF,设EF的中点为G,当点E从点B运动到点A时,点G移动的路径的长是$\sqrt{5}$.
如图,在矩形ABCD中,点P在AD上,AB=2,AP=1,E是AB上的一个动点,连接PE,过点P作PE的垂线,交BC于点F,连接EF,设EF的中点为G,当点E从点B运动到点A时,点G移动的路径的长是$\sqrt{5}$.