题目内容
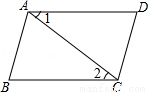
11. 如图,在直角三角形ABC中,AC≠AB,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )
如图,在直角三角形ABC中,AC≠AB,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 由“直角三角形的两锐角互余”,结合题目条件,得∠C=∠BDF=∠BAD=∠ADE.
解答 解:∵AD是斜边BC上的高,DE⊥AC,DF⊥AB,
∴∠C+∠B=90°,∠BDF+∠B=90°,∠BAD+∠B=90°,
∴∠C=∠BDF=∠BAD,
∵∠DAC+∠C=90°,∠DAC+∠ADE=90°,
∴∠C=∠ADE,
∴图中与∠C(除之C外)相等的角的个数是3,
故选:A.
点评 此题考查了直角三角形的性质,余角的性质,掌握直角三角形的两锐角互余是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
20.下列运算正确的是( )
| A. | $\sqrt{6}$÷$\sqrt{2}$=3 | B. | 8$\sqrt{3}$×2$\sqrt{3}$=16$\sqrt{3}$ | C. | 4$\sqrt{3}$×3$\sqrt{2}$=7$\sqrt{6}$ | D. | 2$\sqrt{10}$÷$\sqrt{5}$=2$\sqrt{2}$ |
1.若x2-4x+b=(x-2)(x-a),则a-b的值是( )
| A. | -2 | B. | -6 | C. | 6 | D. | 2 |