题目内容
1．若x2-4x+b=（x-2）（x-a），则a-b的值是（ ）| A． | -2 | B． | -6 | C． | 6 | D． | 2 |
分析 已知等式右边利用多项式乘以多项式法则计算，再利用多项式相等的条件求出a与b的值，即可确定出a-b的值．
解答 解：∵x2-4x+b=（x-2）（x-a）=x2-（a+2）x+2a，
∴a+2=4，b=2a，
解得：a=2，b=4，
则a-b=2-4=-2．
故选A．
点评 此题考查了因式分解-十字相乘法，熟练掌握十字相乘的方法是解本题的关键．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
如图，在直角三角形ABC中，AC≠AB，AD是斜边上的高，DE⊥AC，DF⊥AB，垂足分别为E、F，则图中与∠C（∠C除外）相等的角的个数是（ ）
12．
如图，在甲、乙两地之间要修一条公路，从甲地测得公路的走向是北偏东55°，如果甲、乙两地同时开工，要使公路准确接通，那么在乙地公路施工时∠β的度数应该为（ ）
如图，在甲、乙两地之间要修一条公路，从甲地测得公路的走向是北偏东55°，如果甲、乙两地同时开工，要使公路准确接通，那么在乙地公路施工时∠β的度数应该为（ ）| A． | 135° | B． | 125° | C． | 55° | D． | 35° |
9．使分式$\frac{（x+2）（x-2）}{（x+2）}$有意义的条件是（ ）
| A． | x≠0 | B． | x≠-2 | C． | x≠2 | D． | x可取任意实数 |
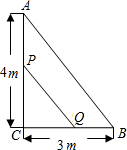如图所示，在Rt△ABC中，点P，Q同时由A，B两点出发分别沿射线AC，BC方向匀速运动，其速度均为2cm/s，当△PCQ的面积是△ABC的面积的一半时，所用的时间为3或0.5s．