题目内容
17.解下列方程:(1)2(x-3)2=x(x-3);
(2)x2-2x-4=0.
分析 (1)首先移项,把方程的右边化成0,左边分解因式,即可化成两个一元一次方程,即可求解;
(2)利用配方法求出解即可.
解答 解:(1)∵2(x-3)2=x(x-3),
∴(x-3)[2(x-3)-x]=0,
∴x-3=0,2(x-3)-x=0,
解得:x1=3,x2=6;
(2)∵x2-2x-4=0,
∴x2-2x=4,
∴x2-2x+1=5,
∴(x-1)2=5,
解得:x1=$\sqrt{5}$+1,x2=-$\sqrt{5}$+1.
点评 本题考查了因式分解法解一元二次方程,正确理解因式分解法的基本思想是化成一元一次方程.

练习册系列答案
相关题目
8.下列运算中正确的是( )
| A. | $\sqrt{4}$+$\sqrt{9}$=$\sqrt{13}$ | B. | $\sqrt{2}$($\sqrt{8}$-$\sqrt{2}$)=$\sqrt{2}$•$\sqrt{6}$=$\sqrt{12}$ | C. | $\sqrt{4}$=±2 | D. | |$\sqrt{2}$-$\sqrt{3}$|=$\sqrt{3}$-$\sqrt{2}$ |
5.设A=3x2-x+1,B=2x2-x-1,若x取任意实数,则A与B的大小关系为( )
| A. | A>B | B. | A=B | C. | A<B | D. | 无法比较 |
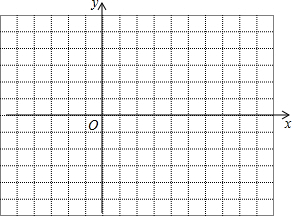 如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点. 如图,在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的角平分线交AD于点E,交CD的延长线于点F,则DE=3cm.
如图,在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的角平分线交AD于点E,交CD的延长线于点F,则DE=3cm.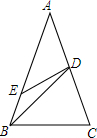 已知:在△ABC中,AB=AC,点D、E分别在在AC、AB上,且BD=BC,BE=DE=AD,求∠C的度数.
已知:在△ABC中,AB=AC,点D、E分别在在AC、AB上,且BD=BC,BE=DE=AD,求∠C的度数.