��Ŀ����
17����ѧ���⣺����$\frac{1}{m}$+$\frac{1}{{m}^{2}}$+$\frac{1}{{m}^{3}}$+��+$\frac{1}{{m}^{n}}$������m��n��������������m��2��n��1��̽�����⣺Ϊ����������ѧ���⣬�����������ν�ϵ�˼�뷽����ͨ�����ϵطָ�һ�����Ϊ1�������Σ���������ϵ�ͼ���ͼ������ؽ������������ȡһ���������⻯�IJ���������̽����
̽��һ������̽��һ������$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+��+$\frac{1}{{2}^{n}}$��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ$\frac{1}{2}$
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ $\frac{1}{2}$+$\frac{1}{{2}^{2}}$��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ȷ֣�������Ӱ���ֵ����֮��Ϊ$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+��+$\frac{1}{{2}^{n}}$���հײ��ֵ������ $\frac{1}{{2}^{n}}$��

̽����������$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+��+$\frac{1}{{3}^{n}}$��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ$\frac{2}{3}$��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ$\frac{2}{3}$+$\frac{2}{{3}^{2}}$��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ����������ȷ֣�������Ӱ���ֵ����֮��Ϊ$\frac{2}{3}$+$\frac{2}{{3}^{2}}$+$\frac{2}{{3}^{3}}$+��+$\frac{2}{{3}^{n}}$�����հײ��ֵ������$\frac{1}{{3}^{n}}$��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��$\frac{2}{3}$+$\frac{2}{{3}^{2}}$+$\frac{2}{{3}^{3}}$+��+$\frac{2}{{3}^{n}}$=1-$\frac{1}{{3}^{n}}$��
����ͬ����2����$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+��+$\frac{1}{{3}^{n}}$=$\frac{1}{2}$-$\frac{1}{2��{3}^{n}}$��

̽����������$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+��+$\frac{1}{{4}^{n}}$��
��1�ηָ�������ε�����ĵȷ֣�������Ӱ���ֵ����Ϊ$\frac{3}{4}$��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ĵȷ֣���Ӱ���ֵ����֮��Ϊ$\frac{3}{4}$+$\frac{3}{{4}^{2}}$��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ĵȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ��������ĵȷ֣�������Ӱ���ֵ����֮��Ϊ$\frac{3}{4}$+$\frac{3}{{4}^{2}}$+$\frac{3}{{4}^{3}}$+��+$\frac{3}{{4}^{n}}$�����հײ��ֵ������$\frac{1}{{4}^{n}}$
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��$\frac{3}{4}$+$\frac{3}{{4}^{2}}$+$\frac{3}{{4}^{3}}$+��+$\frac{3}{{4}^{n}}$=1-$\frac{1}{{4}^{n}}$��
����ͬ����3����$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+��+$\frac{1}{{4}^{n}}$=$\frac{1}{3}$-$\frac{1}{3��{4}^{n}}$

̽���ģ�����$\frac{1}{5}$+$\frac{1}{{5}^{2}}$+$\frac{1}{{5}^{3}}$+��+$\frac{1}{{5}^{n}}$
����������������ֻ������n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ�����������д��̽�����̣�

������⣺����$\frac{1}{m}$+$\frac{1}{{m}^{2}}$+$\frac{1}{{m}^{3}}$+��+$\frac{1}{{m}^{n}}$��
��ֻ�軭����n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ��������������������գ�
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��$\frac{m-1}{m}$+$\frac{m-1}{{m}^{2}}$+$\frac{m-1}{{m}^{3}}$+��+$\frac{m-1}{{m}^{n}}$=1-$\frac{1}{{m}^{n}}$��
���ԣ�$\frac{1}{m}$+$\frac{1}{{m}^{2}}$+$\frac{1}{{m}^{3}}$+��+$\frac{1}{{m}^{n}}$=$\frac{1}{m-1}$-$\frac{1}{��m-1��{m}^{n}}$��
�ع�Ӧ�ã�����$\frac{6-1}{6}$+$\frac{{6}^{2}-1}{{6}^{2}}$+$\frac{{6}^{3}-1}{{6}^{3}}$+��$\frac{{6}^{n}-1}{{6}^{n}}$��
���� ̽���ģ��������ε������ȷ֣���Ӱ���ֵ������������ͼ��ɣ�
������⣺�������ε����m�ȷ֣���Ӱ���ֵ������������ͼ��ɣ�
�ع�Ӧ�ã��Ƚ�����ʽ�ӽ��б��Σ�����1-$\frac{1}{6}$+1-$\frac{1}{{6}^{2}}$+1-$\frac{1}{{6}^{3}}$+��+1-$\frac{1}{{6}^{n}}$����������������ã�$\frac{1}{6}$+$\frac{1}{{6}^{2}}$+$\frac{1}{{6}^{3}}$+��+$\frac{1}{{6}^{n}}$=$\frac{1}{5}$-$\frac{1}{5��{6}^{n}}$�����뼴�ɣ�
��� �⣺̽���ģ�����$\frac{1}{5}$+$\frac{1}{{5}^{2}}$+$\frac{1}{{5}^{3}}$+��+$\frac{1}{{5}^{n}}$��
��1�ηָ�������ε������ȷ֣�������Ӱ���ֵ����Ϊ$\frac{4}{5}$��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ����������ȷ֣���Ӱ���ֵ����֮��Ϊ$\frac{4}{5}+\frac{4}{{5}^{2}}$��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ȷ֣�������Ӱ���ֵ����֮��Ϊ$\frac{4}{5}+\frac{4}{{5}^{2}}+\frac{4}{{5}^{3}}+��+\frac{4}{{5}^{n}}$�����հײ��ֵ������$\frac{1}{{5}^{n}}$��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��$\frac{4}{5}+\frac{4}{{5}^{2}}+\frac{4}{{5}^{3}}+��+\frac{4}{{5}^{n}}$=1-$\frac{1}{{5}^{n}}$��
����ͬ����4����$\frac{1}{5}$+$\frac{1}{{5}^{2}}$+$\frac{1}{{5}^{3}}$+��+$\frac{1}{{5}^{n}}$=$\frac{1}{4}$-$\frac{1}{4��{5}^{n}}$��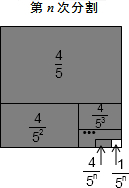
������⣺����$\frac{1}{m}$+$\frac{1}{{m}^{2}}$+$\frac{1}{{m}^{3}}$+��+$\frac{1}{{m}^{n}}$��
��1�ηָ�������ε����m�ȷ֣�������Ӱ���ֵ����Ϊ$\frac{m-1}{m}$��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ��������m�ȷ֣���Ӱ���ֵ����֮��Ϊ$\frac{m-1}{m}$+$\frac{m-1}{{m}^{2}}$��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ��������m�ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ�������m�ȷ֣�������Ӱ���ֵ����֮��Ϊ$\frac{m-1}{m}$+$\frac{m-1}{{m}^{2}}$+$\frac{m-1}{{m}^{3}}$+��+$\frac{m-1}{{m}^{n}}$�����հײ��ֵ������$\frac{1}{{m}^{n}}$��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��$\frac{m-1}{m}$+$\frac{m-1}{{m}^{2}}$+$\frac{m-1}{{m}^{3}}$+��+$\frac{m-1}{{m}^{n}}$=1-$\frac{1}{{m}^{n}}$��
����ͬ����m-1����$\frac{1}{m}$+$\frac{1}{{m}^{2}}$+$\frac{1}{{m}^{3}}$+��+$\frac{1}{{m}^{n}}$=$\frac{1}{m-1}$-$\frac{1}{��m-1��{m}^{n}}$��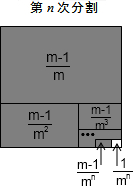
�ʴ�Ϊ��$\frac{m-1}{m}$+$\frac{m-1}{{m}^{2}}$+$\frac{m-1}{{m}^{3}}$+��+$\frac{m-1}{{m}^{n}}$=1-$\frac{1}{{m}^{n}}$��$\frac{1}{m-1}$-$\frac{1}{��m-1��{m}^{n}}$��
�ع�Ӧ�ã�ͬ���ɵã�$\frac{1}{6}$+$\frac{1}{{6}^{2}}$+$\frac{1}{{6}^{3}}$+��+$\frac{1}{{6}^{n}}$=$\frac{1}{5}$-$\frac{1}{5��{6}^{n}}$��
����$\frac{6-1}{6}$+$\frac{{6}^{2}-1}{{6}^{2}}$+$\frac{{6}^{3}-1}{{6}^{3}}$+��$\frac{{6}^{n}-1}{{6}^{n}}$��
=1-$\frac{1}{6}$+1-$\frac{1}{{6}^{2}}$+1-$\frac{1}{{6}^{3}}$+��+1-$\frac{1}{{6}^{n}}$��
=n-��$\frac{1}{6}$+$\frac{1}{{6}^{2}}$+$\frac{1}{{6}^{3}}$+��+$\frac{1}{{6}^{n}}$����
=n-��$\frac{1}{5}$-$\frac{1}{5��{6}^{n}}$����
=n-$\frac{1}{5}$+$\frac{1}{5��{6}^{n}}$��
���� ������ͼ����ı仯�����⣬������ʽ�ĺ�ת��Ϊ�����ε���������������ν�ϵ�˼�����εó����ۣ��������ƹ��Ӧ�ã�

 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�| A�� | 1 | B�� | -2 | C�� | 2��-1 | D�� | -2��1 |
 ��ͼ������ABCD�У�AD��BC��AB=AC��AB��AC����BDC=75�㣬���ABD�Ķ�����
��ͼ������ABCD�У�AD��BC��AB=AC��AB��AC����BDC=75�㣬���ABD�Ķ�����