题目内容
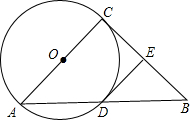 如图,以Rt△ABC的直角边AC为直径作⊙O,交AB于D,E为BC中点,求证:DE是⊙O的切线.
如图,以Rt△ABC的直角边AC为直径作⊙O,交AB于D,E为BC中点,求证:DE是⊙O的切线.考点:切线的判定
专题:证明题
分析:如图,作辅助线;由题意知直线DE经过半径OD的外端,故只要证明OD⊥DE即可.
解答: 证明:如图,连接OD、OE;
证明:如图,连接OD、OE;
∵OA=OC,EC=EB,
∴OE∥AB,
∴∠COE=∠A;∠EOD=∠ADO
又∵OA=OD,
∴∠A=∠ODA;
∴∠COE=∠EOD;
在△COE与△DOE中,
∵
,
∴△COE≌△DOE,
∴∠ODE=∠OCE;
∵∠OCE=90°,
∴∠ODE=90°,
∴DE为⊙O的切线.
 证明:如图,连接OD、OE;
证明:如图,连接OD、OE; ∵OA=OC,EC=EB,
∴OE∥AB,
∴∠COE=∠A;∠EOD=∠ADO
又∵OA=OD,
∴∠A=∠ODA;
∴∠COE=∠EOD;
在△COE与△DOE中,
∵
|
∴△COE≌△DOE,
∴∠ODE=∠OCE;
∵∠OCE=90°,
∴∠ODE=90°,
∴DE为⊙O的切线.
点评:本题主要考查了切线的判定问题;解题的关键是根据题意结合图形正确选用证明方法.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
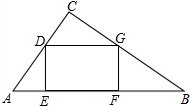 如图,在△ABC中,∠C=90°,AC=6,BC=8,四边形DEFG是它的内接矩形,点D在边AC上,点E、F在边AB上,点G在边BC上,当CD=
如图,在△ABC中,∠C=90°,AC=6,BC=8,四边形DEFG是它的内接矩形,点D在边AC上,点E、F在边AB上,点G在边BC上,当CD=
 如图,△ABC中,∠C=90°,BC=5,O为△ABC的内心,若OC=
如图,△ABC中,∠C=90°,BC=5,O为△ABC的内心,若OC= 如图,以点O为旋转中心,将△ABC按顺时针方向旋转60°,作出旋转后的图形.(保留作图痕迹)
如图,以点O为旋转中心,将△ABC按顺时针方向旋转60°,作出旋转后的图形.(保留作图痕迹)