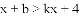题目内容
如图,以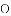
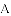
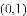

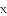
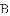
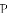
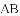
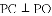

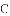
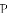
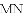
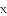
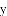
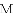

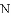
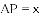
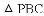
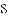
(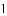
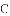
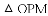
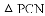
(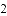
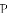
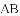
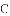

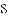
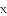
(
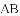
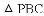
练习册系列答案
相关题目


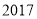 年中秋国庆又在一起放假啦!我国人们旅游热情高涨,小振老师喜欢自驾游,他统计了在
年中秋国庆又在一起放假啦!我国人们旅游热情高涨,小振老师喜欢自驾游,他统计了在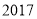 年双节期间,全国自驾游(跨市)游客达到
年双节期间,全国自驾游(跨市)游客达到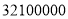 人次,将
人次,将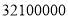 用科学记数法表示应为( ).
用科学记数法表示应为( ).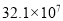 B.
B. 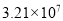 C.
C. 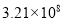 D.
D. 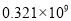
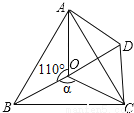
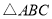 的内切圆,点
的内切圆,点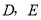 分别为边
分别为边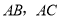 上的点,且
上的点,且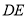 为⊙I的切线,若
为⊙I的切线,若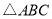 的周长为21,
的周长为21,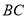 边的长为6,
边的长为6,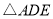 的周长为 .
的周长为 .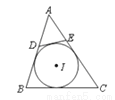
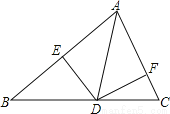
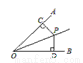
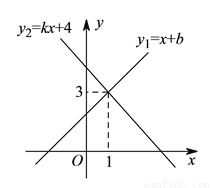
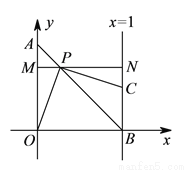
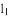 经过点
经过点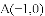
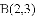
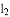 经过点
经过点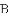
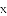
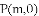
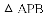

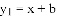 与一次函数
与一次函数 的图象交于点
的图象交于点