题目内容
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连结BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
(1)△OBC与△ABD全等吗?判断并证明你的结论;
(2)将等边△AOB沿x轴翻折,B点的对称点为B′.
①点B′会 落在直线DE上么?请说明理由;
落在直线DE上么?请说明理由;
 ②随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求直接写出点E的坐标;若有变化,请说明理由.
②随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求直接写出点E的坐标;若有变化,请说明理由.
(1)△OBC与△ABD全等,理由如下:
∵△AOB是等边三角形,∴OB=AB,∠OBA=∠OAB=60°,又∵△CBD是等边三角形;∴BC=BD,∠CBD=60°,∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,
在△OBC和△ABD中,
 ,∴△OBC≌△ABD(SAS).
,∴△OBC≌△ABD(SAS).
(2)①点B'会落在直线DE上.
由(1)得,∠BAD=∠AOB=60°,从而得∠CAD=60°,所以∠OAE=60°.
所以∠OAB=∠OAE,所以,点B'会落在直线DE上.
②∵△OBC≌△ABD,∵∠BAD=∠BOC=60°,又∵∠OAB=60°,∴∠O AE=180°-∠OAB-∠BAD=60°,∴Rt△OEA中,AE=2OA=2,
AE=180°-∠OAB-∠BAD=60°,∴Rt△OEA中,AE=2OA=2,
∴OE= ,∴点E的位置不会发生变化,E的坐标为E
,∴点E的位置不会发生变化,E的坐标为E .
.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

 、
、 、
、 、
、 中,无理数的个数有………………( )
中,无理数的个数有………………( ) T的面积分别为
T的面积分别为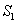 、
、 、
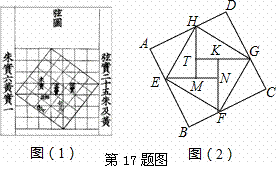
、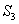 .若正方形EFGH的边长为2,则
.若正方形EFGH的边长为2,则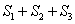 = .
= .

 的绝对值的相反数是_______.
的绝对值的相反数是_______. =3,
=3, =2,且
=2,且 =-xy,则x+y等于_______.
=-xy,则x+y等于_______. ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来.