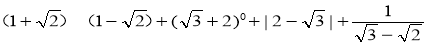题目内容
(本题满分9分)如图,在 中,
中, ,点
,点 从点
从点 开始沿
开始沿 边向点
边向点 以
以 /秒的速度移动,点
/秒的速度移动,点 从点
从点 开始沿
开始沿 边向点
边向点 以
以 /秒的速度移动.
/秒的速度移动.

(1)如果 、
、 分别从
分别从 、
、 同时出发,几秒后
同时出发,几秒后 是等腰三角形?
是等腰三角形?
(2)如果 、
、 分别从
分别从 、
、 同时出发,几秒后
同时出发,几秒后 的面积等于
的面积等于 ?
?
(3)如果 、
、 分别从
分别从 、
、 同时出发,四边形
同时出发,四边形 的面积是
的面积是 面积的三分之二?
面积的三分之二?
(1)2秒;(2)3秒;(3)2秒
【解析】
试题分析:(1)由图知, ,若要
,若要 是等腰三角形,则必定是两直角边相等,设好时间后构造方程求解即可;(2)根据直角三角形面积计算公式构造方程求解即可;(3)四边形面积不易计算,但可转化为两个直角三角形
是等腰三角形,则必定是两直角边相等,设好时间后构造方程求解即可;(2)根据直角三角形面积计算公式构造方程求解即可;(3)四边形面积不易计算,但可转化为两个直角三角形 和
和 的面积关系,再代入直角三角形面积公式计算.
的面积关系,再代入直角三角形面积公式计算.
试题解析:(1) 且
且 是等腰三角形
是等腰三角形  必定是
必定是
设经过 秒后,则
秒后,则 ,
, ,
, ,
,


 2秒后
2秒后 是等腰三角形.
是等腰三角形.
(2)

解得


 (舍)
(舍) 
 3秒后
3秒后 的面积等于
的面积等于 .
.
(3)


 解得
解得 (舍)
(舍) 
 2秒后四边形
2秒后四边形 的面积是
的面积是 面积的三分之二.
面积的三分之二.
考点:1.动点的处理;2.直角三角形的性质;3.解一元二次方程.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目


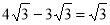 (B)
(B)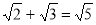
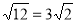 (D)3+
(D)3+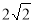 =
=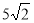


 (配方法)
(配方法)  (公式法)
(公式法)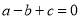 ,
,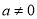 ,则方程
,则方程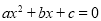 必有一个根是_______.
必有一个根是_______.