��Ŀ����
18�����г��з�ò�����������ڻ��Ƚ����У�����з���һЩ�ƾɵĹ�������ͤ�а���հ����������һ���µĹ�������ͤ���鿴�����ϵ�һЩ��ͤͼƬ�����ʦ������������ʾ��ͼ��AB��FG��Ϊˮƽ�߶Σ�CD��AB��PQ��FG��E��HΪ���㣬��AE=FH��AB=FG=2�ף�ͼ1��tanA=$\frac{2}{5}$��tanB=$\frac{3}{5}$��ͼ2��P�ڻ�FG�ϣ��һ�FG����Բ��Բ��O��FG��PQ�ľ���֮��Ϊ5��2����1����ͼ1�е�CE����
��2����ͼ2�е�PH����
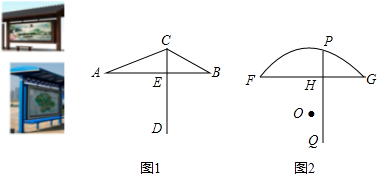
���� ��1���ȸ�����֪�����ó�$\frac{2}{5}$AE=$\frac{3}{5}$BE���ٸ���AE+BE=2�����AE�ij���������CE�ij����ɣ�
��2��������OF��OP������O��FG�Ĵ��ߣ���PQ�Ĵ��ߣ�����ֱ�������Σ��ٸ��ݹ��ɶ������OF�ij��������õ�OP���������ݹ��ɶ������PN�ij������������߶εĺͲ��ϵ�õ�PH�ij���
��� �⣺��1����tanA=$\frac{2}{5}$=$\frac{CE}{AE}$��tanB=$\frac{3}{5}$=$\frac{CE}{BE}$
��CE=$\frac{2}{5}$AE��CE=$\frac{3}{5}$BE
��$\frac{2}{5}$AE=$\frac{3}{5}$BE
�֡�AB=AE+BE=2
��AE=1.2
��CE=1.2��$\frac{2}{5}$=0.48��m��
��2������O��FG�Ĵ��ߣ�����ΪM������O��PQ�Ĵ��ߣ�����ΪN����
FM=1��MH=ON=1.2-1=0.2
��O��FG��PQ�ľ���֮��Ϊ5��2
��OM=0.5=NH
����OF��OP����
ֱ��������OFM�У�OF=$\sqrt{{1}^{2}+0��{5}^{2}}$=$\frac{{\sqrt{5}}}{2}$=OP
��ֱ��������OPN�У�PN=$\sqrt{O{P}^{2}-O{N}^{2}}$=1.1
��PH=PN-NH=1.1-0.5=0.6��m��
���� ������Ҫ�����˽�ֱ�������Σ��������Ĺؼ���ͨ���������߹���ֱ�������Σ���ʵ������ת��Ϊ��ѧ���⣮����ʱ��Ҫ�ۺ�����������Ǻ����������Լ����ɶ�����֪ʶ��

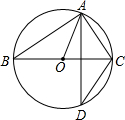 ��ͼ��A��D�ǡ�O�ϵ������㣬BC��ֱ��������D=32�㣬���OAC=��������
��ͼ��A��D�ǡ�O�ϵ������㣬BC��ֱ��������D=32�㣬���OAC=��������| A�� | 64�� | B�� | 58�� | C�� | 72�� | D�� | 55�� |
| A�� | ��1��2�� | B�� | ��-1��-2�� | C�� | ��2��-1�� | D�� | ��2��1�� |

 ��ͼ��A��B����ת�̷ֱ�ƽ���ֳ��������ĸ����Σ��ֱ�ת��A�̡�B�̸�һ�Σ�ת�������У�ָ�뱣�ֲ��������ָ��ǡ��ָ�ڷָ����ϣ�����תһ�Σ�ֱ��ָ��ָ��һ���������ڵ�����Ϊֹ������ת��ֹͣ��ָ����ָ�����ڵ�����֮��С��6�ĸ�����$\frac{1}{2}$��
��ͼ��A��B����ת�̷ֱ�ƽ���ֳ��������ĸ����Σ��ֱ�ת��A�̡�B�̸�һ�Σ�ת�������У�ָ�뱣�ֲ��������ָ��ǡ��ָ�ڷָ����ϣ�����תһ�Σ�ֱ��ָ��ָ��һ���������ڵ�����Ϊֹ������ת��ֹͣ��ָ����ָ�����ڵ�����֮��С��6�ĸ�����$\frac{1}{2}$��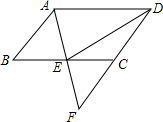 ��ͼ����?ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��
��ͼ����?ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��