题目内容
20.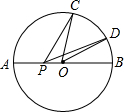 如图,已知⊙O的半径为R,C、D在直径AB的同侧半圆上,∠AOC=96°,∠BOD=36°,动点P在直径AB上,则CP+PD的最小值是( )
如图,已知⊙O的半径为R,C、D在直径AB的同侧半圆上,∠AOC=96°,∠BOD=36°,动点P在直径AB上,则CP+PD的最小值是( )| A. | 2R | B. | $\sqrt{3}$R | C. | $\sqrt{2}$R | D. | R |
分析 首先要确定点P的位置,作点C关于AB的对称点C′,连接C′D,交圆于点P,则点P即为所求作的点.且此时PC+PD的最小值为C′D.
解答 解:作点C关于AB的对称点C′,连接DC′,
根据题意以及垂径定理,
得弧C′D的度数是120°,
则∠C′OD=120度.
作OE⊥C′D于E,
则∠DOE=60°,则
DE=$\frac{\sqrt{3}}{2}$R,
C′D=$\sqrt{3}$R.
故选B.
点评 此类题只要是能够正确确定点P的位置.此题综合运用了垂径定理、勾股定理进行计算.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
7.设点A(x1,y1)和点B(x2,y2)是反比例函数y=$\frac{k}{x}$图象上的两点,当x1<x2<0时,y1>y2,则一次函数y=-2x+k的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.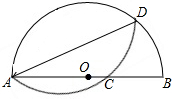 如图,半圆的直径AB=10cm,把弓形沿AD对折,交直径AB于C.若AC=6,则AD的长( )
如图,半圆的直径AB=10cm,把弓形沿AD对折,交直径AB于C.若AC=6,则AD的长( )
 如图,半圆的直径AB=10cm,把弓形沿AD对折,交直径AB于C.若AC=6,则AD的长( )
如图,半圆的直径AB=10cm,把弓形沿AD对折,交直径AB于C.若AC=6,则AD的长( )| A. | 4$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4 |
5.下列运算有错误的是( )
| A. | $\frac{1}{3}$÷(-3)=3×(-3) | B. | (-5)÷(-$\frac{1}{2}$)=-5×(-2) | C. | 5-(-2)=5+2 | D. | 2-3=(+2)+(-3) |
9.2014年7月24日钱江晚报报道,教育部官方微信于7月23日发布了《国家学生体质健康标准(2014年修订)》,该标准规定初中及其以上的男生必测引体向上.为响应该规定,石家庄市某中学的体育老师在体育课上对七年级(1)班的全体男生进行了引体向上的体能测试,每个男生做引体向上的个数不低于5个视为合格,否则就视为不合格.现以每个男生做5个引体向上为标准,超过标准的个数用正数表示,不足标准的个数用负数表示,该体育老师选取了其中8名男生的成绩,记录如下:
(1)该测试合格的有多少名?
(2)这8名男生一共做了多少个引体向上?
| 学生 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 成绩(个) | 1 | 0 | 2 | -1 | 4 | -2 | 0 | 3 |
(2)这8名男生一共做了多少个引体向上?
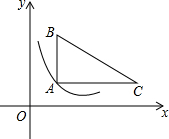 如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.