题目内容
化简：
（1）（4x2y-3xy2）-（1+4x2y-3xy2）
（2）3（4x2-3x+2）-2（1-4x2+x）
（1）（4x2y-3xy2）-（1+4x2y-3xy2）
（2）3（4x2-3x+2）-2（1-4x2+x）
考点：整式的加减
专题：
分析：（1）先去括号，然后合并同类项；
（2）先去括号，然后合并同类项．
（2）先去括号，然后合并同类项．
解答：解：（1）原式=4x2y-3xy2-1-4x2y+3xy2
=-1；
（2）原式=12x2-9x+6-2+8x2-2x
=20x2-11x+4．
=-1；
（2）原式=12x2-9x+6-2+8x2-2x
=20x2-11x+4．
点评：本题考查了整式的加减，解答本题的关键是掌握去括号法则和合并同类项法则．
练习册系列答案
相关题目
已知一元二次方程ax2+bx+c=0（a≠0）中．下列说法：①若a+b+c=0，则b2-4ac≥0；②若方程两根为-1和2，则2a+c=0；③若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根；④若b=2a+3c，则方程有两个不相等的实根．其中结论正确的有（ ）个．
| A、1个 | B、2个 | C、3个 | D、4个 |
已知关于x的方程x2-（2k+1）x+4（k-
）=0．
（1）求证：无论k为何值时，方程总有两个实数根．
（2）若等腰△ABC的一边长a=4，另两边b、c恰好是这个方程的两个实数根，求△ABC的周长．
| 1 |
| 2 |
（1）求证：无论k为何值时，方程总有两个实数根．
（2）若等腰△ABC的一边长a=4，另两边b、c恰好是这个方程的两个实数根，求△ABC的周长．
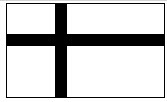如图，要设计一幅长与宽分别为30cm，20cm的图案，其中有两条彩带，横竖彩带宽度相等，如果要使彩带所占面积是图案面积的
如图，Rt△ABC中，CD是斜边AB上的高．
写出图中所有小于平角的角，其中O是直线AB上的一点．