Question

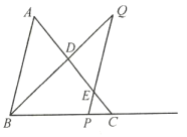
【题目】如图，四边形ABCD中，AC⊥BD垂足为点E，点F，M分别是AB，BC的中点，BN平分∠ABE交AM于点N，AB＝AC＝BD，连接NF．

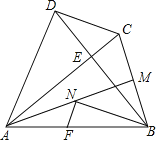
（1）判断线段MN与线段BM的位置关系与数量关系，说明理由；

（2）如果CD＝5，求NF的长．

Answer 1

【答案】（1）位置关系：MN⊥BM，数量关系：MN＝BM，理由见解析；（2）NF＝．

【解析】

（1）根据AB=AC，点M是BC的中点，可证MN⊥BM，AM平分∠BAC，再根据BN平分∠ABE可得出∠MNB的度数，从而可得MN=BM；

（2）连接FM，可证FM∥AC，FM＝AC，从而可得，结合（1）可得，再根据等式的性质通过倒角的关系可知∠NMF＝∠CBD，从而可证△MFN∽△BDC，从而即可求出答案.

（1）位置关系：MN⊥BM，数量关系：MN＝BM，

理由如下：∵AB＝AC，点M是BC的中点，

∴AM⊥BC，AM平分∠BAC，

即MN⊥BM，

∵BN平分∠ABE，

∴∠EBN＝∠ABN，

∵AC⊥BD，

∴∠AEB＝90°，

∴∠EAB+∠EBA＝90°，

∴∠MNB＝∠NAB+∠ABN＝（∠EAB+∠EBA）＝45°，且AM⊥BC，

∴∠MBN＝45°＝∠MNB，

∴MN＝BM；

（2）连接FM，

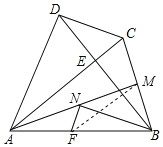
∵点F，M分别是AB，BC的中点，

∴FM∥AC，FM＝AC，

∵AC＝BD，

∴FM＝BD，即，

由（1）知△BMN是等腰直角三角形，

∴MN＝BM＝BC，即，

∴，

∵AM⊥BC，

∴∠NMF+∠FMB＝90°，

∵FM∥AC，

∴∠ACB＝∠FMB，

∵∠CEB＝90°，

∴∠ACB+∠CBD＝90°，

∴∠CBD+∠FMB＝90°，

∴∠NMF＝∠CBD，且，

∴△MFN∽△BDC，

∴，且CD＝5，

∴FN＝．