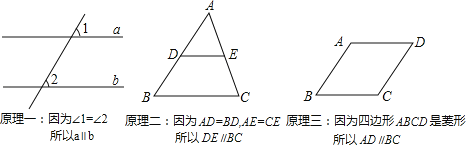
题目内容
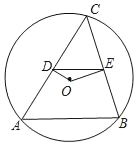
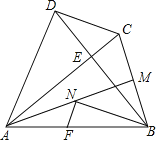
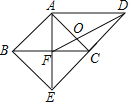
【题目】如图,在平行四边形ABCD中,∠BAC=90°,AB=AC,过点A作边BC的垂线AF交DC的延长线于点E,点F是垂足,连接BE,DF,DF交AC于点O。则下列结论:①四边形ABCD是正方形;②CO:BE=1:3;③DE=![]() BC;④S四边形OCEF=S△AOD 正确的个数是( )
BC;④S四边形OCEF=S△AOD 正确的个数是( )
A.1B.2C.3D.4
【答案】D
【解析】
①先证明△ABF≌△ECF,得AB=EC,再得四边形ABEC为平行四边形,进而由∠BAC=90°,得四边形ABCD是正方形,便可判断正误;
②由△OCF∽△OAD,得OC:OA=1:2,进而得OC:BE的值,便可判断正误;
③根据BC=![]() AB,DE=2AB进行推理说明便可;
AB,DE=2AB进行推理说明便可;
④由△OCF与△OAD的面积关系和△OCF与△AOF的面积关系,便可得四边形OCEF的面积与△AOD的面积关系.
解:①∵∠BAC=90°,AB=AC,
∴BF=CF,
∵四边形ABCD是平行四边形,
∴AB∥DE,
∴∠BAF=∠CEF,
∵∠AFB=∠CFE,
∴△ABF≌△ECF(AAS),
∴AB=CE,
∴四边形ABEC是平行四边形,
∵∠BAC=90°,AB=AC,
∴四边形ABEC是正方形,故此题结论正确;
②∵OC∥AD,
∴△OCF∽△OAD,
∴OC:OA=CF:AD=CF:BC=1:2,
∴OC:AC=1:3,∵AC=BE,
∴OC:BE=1:3,故此小题结论正确;
③∵AB=CD=EC,
∴DE=2AB,
∵AB=AC,∠BAC=90°,
∴AB=![]() BC,
BC,
∴DE=2×![]() ,故此小题结论正确;
,故此小题结论正确;
④∵△OCF∽△OAD,
∴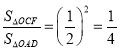 ,
,
∴![]() ,
,
∵OC:AC=1:3,
∴3S△OCF=S△ACF,∵S△ACF=S△CEF,
∴![]() ,
,
∴![]() ,故此小题结论正确.
,故此小题结论正确.
故选:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目