题目内容
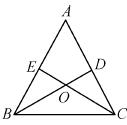
如图,正方形 中,点F在边BC上,E在边BA的延长线上.
中,点F在边BC上,E在边BA的延长线上.

(1)若 按顺时针方向旋转后恰好与
按顺时针方向旋转后恰好与 重合.则旋转中心是点 ;最少旋转了 度;
重合.则旋转中心是点 ;最少旋转了 度;
(2)在(1)的条件下,若 ,求四边形
,求四边形 的面积.
的面积.
(1)D; ;(2)25.
;(2)25.
【解析】
试题分析:(1)△DCF按顺时针方向旋转后恰好与△DAE重合,DA与DC重合,这旋转角为∠CDA=90°,根据旋转的定义得到旋转中心是点 D;最少旋转了 90°;
(2)根据旋转的性质得△DCF≌△DAE,得AE=CF=3,则BC=BF+CF=5,并且S四边形BFDE=S△AED+S四边形ABFD=S△DCF+S四边形ABFD=S正方形ABCD,利用正方形的面积公式即可得到四边形BFDE的面积.
试题解析:(1)D;
(2)∵△DCF旋转后恰好与△DAE重合,
∴△DCF≌△DAE,
∴AE=CF=3,
又∵BF=2,
∴BC=BF+CF=5,
∴S四边形BFDE=S△AED+S四边形ABFD=S△DCF+S四边形ABFD=S正方形ABCD=BC2=25.
考点:1.旋转的性质;2.全等三角形的判定与性质;3.正方形的性质.

练习册系列答案
相关题目

 有两个不相等实数根的概率.
有两个不相等实数根的概率.
 只,甲、乙两人进行摸球游戏:甲先从袋中摸出一球,看清颜色后放回,再由乙从袋中摸出一球.
只,甲、乙两人进行摸球游戏:甲先从袋中摸出一球,看清颜色后放回,再由乙从袋中摸出一球.