题目内容
9.已知|999-a|+$\sqrt{a-1020}$=a,求$\sqrt{{a-999}^{2}+4}$的值.分析 二次根式有意义的条件确定a的范围,根据已知等式求出a的值,代入所求的代数式计算得到答案.
解答 解:∵a-1020≥0,
∴a≥1020,
∴|999-a|+$\sqrt{a-1020}$=a可化为a-999+$\sqrt{a-1020}$=a,
即$\sqrt{a-1020}$=999,
解得,a=9992+1020,
∴原式=$\sqrt{1024}$=32.
点评 本题考查的是二次根式有意义的条件、算术平方根,掌握二次根式有意义的条件是被开方数大于等于0是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.下列调查中,适合用普查(全面调查)方式的是( )
| A. | 了解一批袋装食品是否含有防腐剂 | |
| B. | 了解某班学生“50米跑”的成绩 | |
| C. | 调查我国居民对汽车废气污染环境的看法 | |
| D. | 了解一批灯泡的使用寿命 |

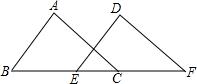 如图,△ABC和△DEF,B、E、C、F在一条直线上,AB=DE,BE=CF,∠B=∠DEF,求证:AC=DF.
如图,△ABC和△DEF,B、E、C、F在一条直线上,AB=DE,BE=CF,∠B=∠DEF,求证:AC=DF.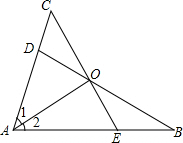 已知:如图,点D、E分别在AC、AB上,BD、CE相交于点O,AC=AB,AD=AE,∠1=∠2,求证:
已知:如图,点D、E分别在AC、AB上,BD、CE相交于点O,AC=AB,AD=AE,∠1=∠2,求证: