题目内容
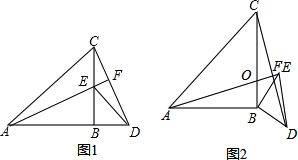
20.将一大、一小两个等腰直角三角形拼接,AB=CB,EB=DB,∠ABC=∠EBD=90°,连接AE,CD(1)如图1,若A,B,D三点共线,试确定AE与CD的位置关系与数量关系,并证明你的结论;
(2)如图2,若A,B,D三点不共线,(1)中的结论是否成立,为什么?
分析 (1)根据题意可以证明△ABE≌△CBD,进而得出∠AEB=∠CDB,AE=CD,据此即可得解;
(2)首先证明∠ABE=∠CBD,可以得出△ABE≌△CBD,进而得出∠EAB=∠DCB,AE=CD,据此即可得解.
解答 解:(1)AE⊥CD,AE=CD,
∵在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABC=∠EBD}\\{EB=DB}\end{array}\right.$,
∴△ABE≌△CBD(ASA),
∴AE=CD,∠AEB=∠CDB,
∵∠AEB+∠EAB=90°,
∴∠CDB+∠EAB=90°,
∴∠AFD=90°,
∴AE⊥CD;
(2)成立,
∵∠ABC=∠EBD=90°,
∴∠ABC+∠CBE=∠EBD+∠CBE,
即:∠ABE=∠CBD,
在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBD}\\{EB=DB}\end{array}\right.$,
∴∴△ABE≌△CBD(ASA),
∴AE=CD,∠EAB=∠DCB,
∵∠AOB+∠EAB=90°,
∴∠DCB+∠COE=90°,
∴∠AFC=90°,
∴AE⊥CD.
点评 本题主要考查了三角形全等的性质定理与判定定理.牢记定理是解题的关键,还考查了垂直的定义,注意总结.

练习册系列答案
相关题目
12.把一元二次方程6x2-3=4x(2x-1)化为一般形式是( )
| A. | -2x2-4x+3=0 | B. | 2x2+4x-3=0 | C. | 2x2-4x+3=0 | D. | 2x2-4x-3=0 |
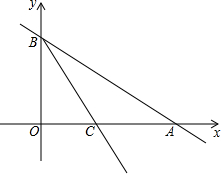 如图,已知A、B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,如果OA,OB的长分别是x2-14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,
如图,已知A、B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,如果OA,OB的长分别是x2-14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,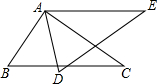 如图,△ABC≌△ADE,则下列结论成立的是( )
如图,△ABC≌△ADE,则下列结论成立的是( )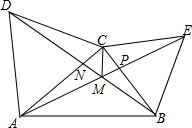 还记得在全等三角形中证明的一个习题吗?如图所示,已知在△ABC中,分别以AC、BC为边,向外作正△ACD、正△BCE,BD与AE相交于M,求证:AE=BD
还记得在全等三角形中证明的一个习题吗?如图所示,已知在△ABC中,分别以AC、BC为边,向外作正△ACD、正△BCE,BD与AE相交于M,求证:AE=BD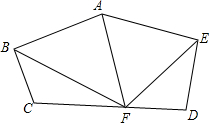 如图,已知AB=AE,BC=ED,∠C=∠D,点F是CD的中点,∠BAF与∠EAF相等吗?为什么?
如图,已知AB=AE,BC=ED,∠C=∠D,点F是CD的中点,∠BAF与∠EAF相等吗?为什么?