题目内容
已知双曲线y=
经过点A(-1,2).
(1)求该反比例函数的解析式;
(2)若B(b,m)、C(c,n)是该双曲线上的两个点,且b<c<0,判断m,n的大小关系;
(3)判断关于x的一元二次方程kx2+2x-1=0的根的情况.
| k |
| x |
(1)求该反比例函数的解析式;
(2)若B(b,m)、C(c,n)是该双曲线上的两个点,且b<c<0,判断m,n的大小关系;
(3)判断关于x的一元二次方程kx2+2x-1=0的根的情况.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征,抛物线与x轴的交点
专题:
分析:(1)根据待定系数法即可求得;
(2)根据反比例函数的性质先判定图象在二、四象限,y随x的增大而增大,根据b<c<0,可以确定B(b,m)、C(c,n)两个点在第四象限,从而判定m,n的大小关系;
(3)根据(1)求得的k的值,一元二次方程为-2x2+2x-1=0,由△=22-4×(-2)×(-1)=-4<0,从而判定
一元二次方程kx2+2x-1=0的根的情况.
(2)根据反比例函数的性质先判定图象在二、四象限,y随x的增大而增大,根据b<c<0,可以确定B(b,m)、C(c,n)两个点在第四象限,从而判定m,n的大小关系;
(3)根据(1)求得的k的值,一元二次方程为-2x2+2x-1=0,由△=22-4×(-2)×(-1)=-4<0,从而判定
一元二次方程kx2+2x-1=0的根的情况.
解答:解:(1)∵双曲线y=
经过点A(-1,2),
∵2=
,解得k=-2,
∴该反比例函数的解析式为y=-
(2)∵k=-2<0,
∴图象在二、四象限,y随x的增大而增大,
又∵b<c<0,
∴B(b,m)、C(c,n)两个点在第四象限,
∴m<n.
(3)∵k=-2,
∴一元二次方程为-2x2+2x-1=0,
∵△=22-4×(-2)×(-1)=-4<0,
∴关于x的一元二次方程kx2+2x-1=0没有实数根.
| k |
| x |
∵2=
| k |
| -1 |
∴该反比例函数的解析式为y=-
| 2 |
| x |
(2)∵k=-2<0,
∴图象在二、四象限,y随x的增大而增大,
又∵b<c<0,
∴B(b,m)、C(c,n)两个点在第四象限,
∴m<n.
(3)∵k=-2,
∴一元二次方程为-2x2+2x-1=0,
∵△=22-4×(-2)×(-1)=-4<0,
∴关于x的一元二次方程kx2+2x-1=0没有实数根.
点评:本题考查了待定系数法求解析式,反比例函数的性质,方程根的情况的判定等,熟练掌握反比例函数的性质是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
已知k1<0<k2,则函数y=k1x和y=
的图象大致是( )
| k2 |
| x |
A、 |
B、 |
C、 |
D、 |
有两个事件,事件A:某射击运动员射击一次,命中靶心;事件B:掷一枚硬币,正面朝上,则( )
| A、事件A和事件B都是随机事件 |
| B、事件A和事件B都是必然事件 |
| C、事件A是随机事件,事件B是必然事件 |
| D、事件A是必然事件,事件B是随机事件 |
将一元二次方程4x2+5x=81化成一般式后,如果二次项系数是4,则一次项系数和常数项分别是( )
| A、5,81 |
| B、5,-81 |
| C、-5,81 |
| D、5x,-81 |
顶点为(6,0),开口向下,开口的大小与函数y=
x2的图象相同的抛物线所对应的函数是( )
| 1 |
| 3 |
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
已知x1,x2是方程x2-5x-2=0的两个实数根,则x12-x1x2+x22的值为( )
| A、31 | B、29 | C、25 | D、17 |
 如图,一只船由原点O出发,航行40海里至A点,接着又航行12海里至B点,已知∠1=60°,∠2=45°,求B点的坐标.
如图,一只船由原点O出发,航行40海里至A点,接着又航行12海里至B点,已知∠1=60°,∠2=45°,求B点的坐标.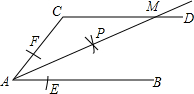 如图,AB∥CD,以点A为圆心,小于AC长为半径画弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
如图,AB∥CD,以点A为圆心,小于AC长为半径画弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于