题目内容

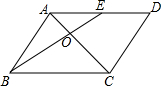如图，在平行四边形ABCD中，点E为边AD的中点，连接AC、BE交于点O，若AO=3，则AC=
 
．
考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：根据平行四边形的性质得到AD∥BC，且AD=BC，易证△AEO∽△CBO，则由该相似三角形的对应边成比例来求AC的长度．
解答：解：如图，∵四边形ABCD是平行四边形，
∴AD∥BC，且AD=BC，
∴△AEO∽△CBO，
∴
AE
BC
=
AO
CO
．
又∵点E为边AD的中点，AO=3，
∴
1
2
=
3
CO
，
∴CO=6，
∴AC=AO+CO=9．
故答案是：9．
点评：本题考查了相似三角形的判定与性质，平行四边形的性质．平行四边形的对边平行且相等的性质，熟记定理并求出OC的比是解题的关键．
练习册系列答案
相关题目
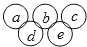在奥运五环图案内，分别填写五个数a，b，c，d，e，如图，，其中a，b，c是三个连续偶数（a＜b），d，e是两个连续奇数（d＜e），且满足a+b+c=d+e，例如：．
（1）请你在0～20之间选择另一组符合条件的数填入图中：．
（2）请你用n（n为自然数）表示三个连续偶数为
 
，
 
，
 
；它们的和为
 
；用m（m为自然数）表示两个连续奇数为
 
，
 
；它们的和为
 
；
（3）对于任选的三个连续偶数，是否都存在两个连续奇数满足上述的填数方法．若存在请说明填数的方法；若不存在，则三个连续偶数正中间的数满足什么条件时一定存在．
通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．
（1）下面是一个案例，请补充完整；
如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则 EF=BE+DF，理由如下：
∵AB=AD，∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
∵∠ADC=∠B=∠ADG=90°，∴∠FDG=180°，点F、D、G共线．
由旋转得：△ABE≌△ADG∴AE=AG，BE=DG，∠BAE=∠DAG
而∠BAE+∠DAF=∠BAD-∠EAF=90°-45°=45°∴∠DAG+∠DAF=45°  即∠FAG=45°
∴∠EAF=∠FAG
根据
 
（填三角形全等的方法），证得
 
≌△AFG，
∴EF=FG
又∵FG=DG+DF
∴EF=DG+DF=BE+DF．
（2）类比引申
如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系
 
 时，仍有EF=BE+DF．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．
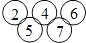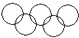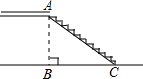如图，市政府准备修建一座的过街天桥，已知地面BC为8米，则桥的坡面AC是10米．则此街道的交通“限高”为
 
米．
计算：
2
1×2
+
2
2×3
+
2
3×4
+…+
2
n(n+1)
=
 
（n为正整数）．
在式子a+b，3xy，
y
x
，n，-8，
m-n
3
，
x
2
中，单项式的个数是（　　）
A、4B、5C、6D、7
在一次捐款中，某班第一组有10名同学，其捐款数额统计如下表：
捐款（元）10152050
人数1432
则捐款数额组成的一组数据中，众数是
 
，中位数是
 
．
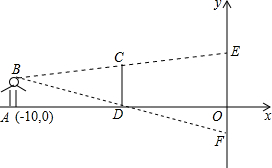如图，在平面直角坐标系内，小聪站在距离y轴10m点A（-10，0）处观察y轴．眼睛距x轴1.5m，他的前方5m处有一障碍物CD，若CD=2m．求y轴上小聪看不到的EF的长，并求出E、F两点的坐标．
已知Rt△ABC中，∠C=90°．
（1）若a=2，c=5，求b；
（2）若c=35，a：b=4：3，求a；
（3）若∠A=60°，a=2，求c．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网