题目内容
 已知AB=10cm,点C是线段AB上的一个动点,点D是线段AC的中点,点E是线段BC上一点,DE=5cm.
已知AB=10cm,点C是线段AB上的一个动点,点D是线段AC的中点,点E是线段BC上一点,DE=5cm.(1)求证:点E是线段BC的中点.
(2)若点C在直线AB上运动,其他条件不变,点E还是BC的中点吗?
考点:两点间的距离
专题:
分析:(1)根据中点的性质,可得DC与AC的关系,根据线段的和差,可得DC与CE、AB的关系,根据等量代换,可得CE与CB的关系;
(2)理由同(1).
(2)理由同(1).
解答:(1)证明∵点D是线段AC的中点,
∴DC=AD=
AC,
∵DE=DC+CE=5=
AB=
(AC+CB),
∴CE+
AC=
AC+
CB,
即CE=
CB,
∴E是BC的中点;
(2)点E还是BC的中点,理由如下:
∵点D是线段AC的中点,
∴DC=AD=
AC,
∵DE=DC+CE=5=
AB=
(AC+CB),
∴CE+
AC=
AC+
CB,
即CE=
CB,
∴E是BC的中点.
∴DC=AD=
| 1 |
| 2 |
∵DE=DC+CE=5=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即CE=
| 1 |
| 2 |
∴E是BC的中点;
(2)点E还是BC的中点,理由如下:
∵点D是线段AC的中点,
∴DC=AD=
| 1 |
| 2 |
∵DE=DC+CE=5=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即CE=
| 1 |
| 2 |
∴E是BC的中点.
点评:本题考查了两点间的距离,利用了线段中点的性质,线段的和差.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,已知Rt△ABC中,∠ACB=90°,AC=3,BC=6.绕点C旋转A′B′经过BC中点E,求B′E.
如图,已知Rt△ABC中,∠ACB=90°,AC=3,BC=6.绕点C旋转A′B′经过BC中点E,求B′E. 如图,△ABC的AB边和AC边上各取一点D和E,且使AD=AE,DE延长线与BC延长线相交于F,求证:
如图,△ABC的AB边和AC边上各取一点D和E,且使AD=AE,DE延长线与BC延长线相交于F,求证: 如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y= ,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如:
,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如: .
. .
.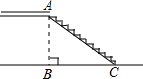 如图,市政府准备修建一座的过街天桥,已知地面BC为8米,则桥的坡面AC是10米.则此街道的交通“限高”为
如图,市政府准备修建一座的过街天桥,已知地面BC为8米,则桥的坡面AC是10米.则此街道的交通“限高”为