题目内容
18.一个二元码是由0和1组成的数字串x1x2…xn(n为正整数),其中xk(k=1,2,…,n)称为第k位码元,如:二元码01101的第1位码元为0,第5位码元为1.(1)二元码100100的第4位码元为1;
(2)二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0).已知某种二元码x1x2…x7的码元满足如下校验方程组:$\left\{\begin{array}{l}{x_2}⊕{x_3}⊕{x_6}⊕{x_7}=1\\{x_4}⊕{x_5}⊕{x_6}⊕{x_7}=1\\{x_1}⊕{x_3}⊕{x_5}⊕{x_7}=1\end{array}\right.$
其中运算⊕定义为:0⊕0=0,1⊕1=0,0⊕1=1,1⊕0=1.
①计算:0⊕1⊕1⊕0=0;
②现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了0101101,那么利用上述校验方程组可判定k等于3.
分析 (1)在二元码100100中,找出第4个数字即可;
(2)①根据“运算⊕定义为:0⊕0=0,1⊕1=0,0⊕1=1,1⊕0=1”,一步步计算即可得出结论;
②将二元码0101101代入方程组,可得出错误出在x2⊕x3、x1⊕x3,结合仅有一个码元错误即可得出k=3.
解答 解:(1)在二元码100100中,第4个数字为1.
故答案为:1.
(2)①0⊕1⊕1⊕0=1⊕1⊕0=0⊕0=0.
故答案为:0.
②∵1⊕0⊕0⊕1=1⊕0⊕1=1⊕1=0,1⊕1⊕0⊕1=0⊕0⊕1=0⊕1=1,0⊕0⊕1⊕1=0⊕1⊕1=1⊕1=0,
∴校验后可知4、5、6、7正确,错误出在x2⊕x3、x1⊕x3.
∵一个这种二元码在通信过程中仅在第k位发生码元错误,
∴k=3.
故答案为:3.
点评 本题考查了二元一次方程组的应用以及新定义,解题的关键是:(1)明白码元的概念;(2)①熟读题意,弄清运算⊕定义;②将错误的二元码代入方程组找出错误出在x2⊕x3、x1⊕x3.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
10.已知a-b=-3,c+d=2,则(b+c)-(a-d)的值为( )
| A. | -1 | B. | -5 | C. | 5 | D. | 1 |
 如图,点M在等边三角形ABC的BC边上,延长BA至N,使AN=MC,连接MN交AC于点O,求证:OM=ON.
如图,点M在等边三角形ABC的BC边上,延长BA至N,使AN=MC,连接MN交AC于点O,求证:OM=ON.
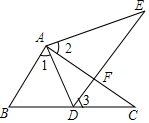 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证:
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证: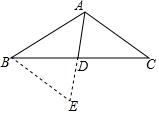 如图,在△ABC中,AD为BC边上中线.若AB=5,AC=7,则AD的取值范围1<AD<6.
如图,在△ABC中,AD为BC边上中线.若AB=5,AC=7,则AD的取值范围1<AD<6.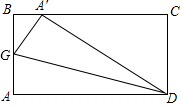 如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′),折痕交AB于点G,则∠ADG=15度.
如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′),折痕交AB于点G,则∠ADG=15度.