题目内容
 在平面直角坐标系xOy中,A(0,4),B(2,0),C(5,1),D(2,5).
在平面直角坐标系xOy中,A(0,4),B(2,0),C(5,1),D(2,5).(1)AD=
(2)∠BAD是直角吗?请说出理由;
(3)求点B到直线CD的距离.
考点:勾股定理,坐标与图形性质,勾股定理的逆定理
专题:
分析:(1)直接根据两点间的距离公式可求出AD及AB的长即可;
(2)连接BD,根据勾股定理的逆定理进行判断即可;
(3)过点B作BE⊥CD于点E,作CE⊥x轴于点G,根据三角形的面积公式求出BE的长即可.
(2)连接BD,根据勾股定理的逆定理进行判断即可;
(3)过点B作BE⊥CD于点E,作CE⊥x轴于点G,根据三角形的面积公式求出BE的长即可.
解答: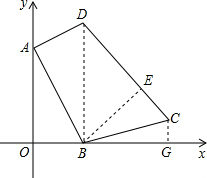 解:(1)∵A(0,4),B(2,0),C(5,1),D(2,5).
解:(1)∵A(0,4),B(2,0),C(5,1),D(2,5).
∴AD=
=
;
AB=
=
=2
.
故答案为:
,2
;
(2)∠BAD是直角.
理由:连接BD,
∵B(2,0),D(2,5),
∴BD=5-0=5.
∵由(1)知AD=
,AB=2
,
∴AD2=5,AB2=20,BD2=25,
∴AD2+AB2=BD2,
∴∠BAD是直角;
(3)过点B作BE⊥CD于点E,作CE⊥x轴于点G,
∵C(5,1),D(2,5),
∴CD=
=5,
∵B(2,0),D(2,5).
∴BD⊥x轴,BG=5-2=3,CG=1,
∴S△BCD=S梯形DBGC-S△BCG,即
×5BE=
(1+5)×3-
×1×3,解得BE=3.
答:点B到直线CD的距离为3.
 解:(1)∵A(0,4),B(2,0),C(5,1),D(2,5).
解:(1)∵A(0,4),B(2,0),C(5,1),D(2,5).∴AD=
| (0-2)2+(4-5)2 |
| 5 |
AB=
| OA2+OB2 |
| 42+22 |
| 5 |
故答案为:
| 5 |
| 5 |
(2)∠BAD是直角.
理由:连接BD,
∵B(2,0),D(2,5),
∴BD=5-0=5.
∵由(1)知AD=
| 5 |
| 5 |
∴AD2=5,AB2=20,BD2=25,
∴AD2+AB2=BD2,
∴∠BAD是直角;
(3)过点B作BE⊥CD于点E,作CE⊥x轴于点G,
∵C(5,1),D(2,5),
∴CD=
| (5-2)2+(1-5)2 |
∵B(2,0),D(2,5).
∴BD⊥x轴,BG=5-2=3,CG=1,
∴S△BCD=S梯形DBGC-S△BCG,即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答:点B到直线CD的距离为3.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
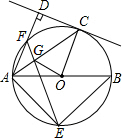 如图,在半径为5的⊙O中,AB是直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
如图,在半径为5的⊙O中,AB是直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D.