Question

2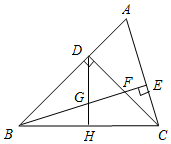．已知：如图，△ABC中，DB=DC，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH与BE相交于点G．
（1）求证：△BDF≌△CDA；
（2）求证：CE=$\frac{1}{2}$BF．

Answer 1

分析 （1）根据ASA证出△BDF≌△CDA即可；
（2）推出∠AEB=∠CEB，∠ABE=∠CBE，根据ASA证出△AEB≌△CEB，推出AE=CE即可．

解答 （1）证明：∵CD⊥AB，BE⊥AC，
∴∠BDF=∠ADC=∠FEC=90°
∵∠DBF=90°-∠BFD，∠DCA=90°-∠EFC，且∠BFD=∠EFC，
∴∠DBF=∠DCA．
在Rt△DFB和Rt△DAC中，
$\left\{\begin{array}{l}{∠BDF=∠ADC}\\{BD=CD}\\{∠DBF=∠ACD}\end{array}\right.$，
∴Rt△DFB≌Rt△DAC（AAS）．

（2）证明：∵BE平分∠ABC，
∴∠ABE=∠CBE．
在Rt△BEA和Rt△BEC中，
$\left\{\begin{array}{l}{∠AEB=∠CEB}\\{BE=BE}\\{∠ABE=∠CBE}\end{array}\right.$，
∴Rt△BEA≌Rt△BEC（ASA）．
∴CE=AE=$\frac{1}{2}$AC．
又由（1），知BF=AC，
∴CE=$\frac{1}{2}$AC=$\frac{1}{2}$BF

点评 本题考查了全等三角形的性质和判定、等腰直角三角形的性质、等腰三角形的判定和性质等知识，关键是推出△BDF≌△CDA和△AEB≌△CEB，属于中考常考题型．