Question

如图，BD、CE是△ABC的中线，P、Q分别是BD、CE的中点，则PQ：BC等于（　　）

• A、1：4
• B、1：5
• C、1：6
• D、1：7

Answer 1

考点：三角形中位线定理

专题：

分析：连接DE，连接并延长EP交BC于点F，利用DE是△ABC中位线，求出FC=

1

2

BC，再用PQ是△EFC中位线，PQ=

1

2

CF，即可求得答案．

解答：解：连接DE，连接并延长EP交BC于点F，
∵DE是△ABC中位线，
∴DE=

1

2

BC，AE=BE，AD=CD，
∴∠EDB=∠DBF，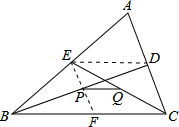
∵P、Q是BD、CE的中点，
∴DP=BP，
∵在△DEP与△BFP中，

∠EDB=∠DBF DP=BP ∠EPD=∠BPF

，
∴△DEP≌△BFP（ASA），
∴BF=DE=

1

2

BC，P是EF中点，
∴FC=

1

2

BC，
PQ是△EFC中位线，
PQ=

1

2

FC，
∴PQ：BC=1：4．
故选A．

点评：此题考查学生对三角形中位线定理的理解与掌握，连接DE，连接并延长EP交BC于点F，求出△DEP≌△BFP，FC=

1

2

BC，是解答此题的关键．