题目内容
3.阅读下列材料:如果我们规定一种运算为$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,例如:$|\begin{array}{l}{2}&{4}\\{3}&{5}\end{array}|$=2×5-4×3=-2,请按照这种运算的规定,解答下列问题:
(1)若$|\begin{array}{l}{5}&{\frac{1}{x-3}}\\{2x}&{\frac{1}{x}}\end{array}|$=-2,求x的值;
(2)当x满足什么条件时,-1<$|\begin{array}{l}{x}&{x-3}\\{3}&{-2}\end{array}|$≤4;
(3)如果规定$|\begin{array}{l}{a}&{b}&{c}\\{d}&{e}&{f}\\{g}&{h}&{i}\end{array}|$=a$|\begin{array}{l}{e}&{f}\\{h}&{i}\end{array}|$-b$|\begin{array}{l}{d}&{f}\\{g}&{i}\end{array}|$+c$|\begin{array}{l}{d}&{e}\\{g}&{h}\end{array}|$,试计算$|\begin{array}{l}{a}&{1}&{1}\\{1}&{a}&{1}\\{1}&{1}&{a}\end{array}|$的值.
分析 (1)利用题中的新定义计算,即可求出x的值;
(2)不等式利用题中的新定义变形,即可求出解集;
(3)利用题中的新定义化简原式,计算即可得到结果.
解答 解:(1)由题中的新定义得:$\frac{5}{x}$-$\frac{2x}{x-3}$=-2,
去分母得:5x-15-2x2=-2x2+6x,
解得:x=-15,
经检验x=-15是分式方程的解;
(2)已知不等式变形得:-1<-2x-3(x-3)≤4,
整理得:1≤x<2;
(3)根据题中的新定义得:原式=a(a2-1)-1×(a-1)+1×(1-a)=a3-a-a+1+1-a=a3-3a+2.
点评 此题考查了解分式方程,以及解一元一次不等式组,弄清题中的新定义是解本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.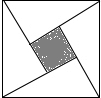 由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
 由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )| A. | 1 | B. | 3 | C. | 4-2$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
8. 已知某几何体的三视图如图所示,则该几何体是( )
已知某几何体的三视图如图所示,则该几何体是( )
 已知某几何体的三视图如图所示,则该几何体是( )
已知某几何体的三视图如图所示,则该几何体是( )| A. | 圆柱 | B. | 棱柱 | C. | 圆锥 | D. | 三棱锥 |
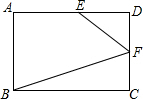 已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF,若AB=4,BC=5,则AE=$\frac{29}{10}$.
已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF,若AB=4,BC=5,则AE=$\frac{29}{10}$. 如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是勾股定理.
如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是勾股定理.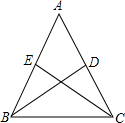 如图,在△ABC中,AB=AC,点E,D分别在AB,AC上,不再添加其他辅助线,添加一个条件AE=AD,使BD=CE(只添一个即可).
如图,在△ABC中,AB=AC,点E,D分别在AB,AC上,不再添加其他辅助线,添加一个条件AE=AD,使BD=CE(只添一个即可).