题目内容
1. 如图,已知D为△ABC的内心,∠A=m,∠D=n,请你探究m、n之间的关系,并证明你的结论.
如图,已知D为△ABC的内心,∠A=m,∠D=n,请你探究m、n之间的关系,并证明你的结论.
分析 由三角形内心定义可知:DB、DC是∠ABC、∠ACB的角平分线.利用内角和定理先求得∠ABC+∠ACB=180°-∠A=180°-m,
所以可知∠DBC+∠DCB=$\frac{1}{2}$(∠ABC+∠ACB),把对应数值代入此关系式即可求得结论.
解答 解:∵DB、DC是∠ABC、∠ACB的角平分线,
∴∠DBC+∠DCB=$\frac{1}{2}$(∠ABC+∠ACB),
∵∠A=m,
∴∠ABC+∠ACB=180°-∠A=180°-m,
∴∠BDC=180°-(∠DBC+∠DCB)=180°+$\frac{1}{2}$m=n,
∴n=180°+$\frac{1}{2}$m.
点评 本题考查了三角形内心的性质:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
11.-8的立方根是( )
| A. | -2$\sqrt{2}$ | B. | ±2 | C. | 2 | D. | -2 |
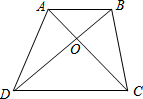 如图,梯形ABCD中,AB∥CD,AB=2,CD=3,若S△AOB=1,则S梯形ABCD=$\frac{25}{4}$.
如图,梯形ABCD中,AB∥CD,AB=2,CD=3,若S△AOB=1,则S梯形ABCD=$\frac{25}{4}$.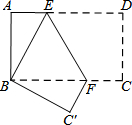 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.



 如图,已知AB:AD=AD:AE=BC:DE,试说明AD•CE=BD•AE.
如图,已知AB:AD=AD:AE=BC:DE,试说明AD•CE=BD•AE.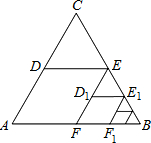 如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.