题目内容
12.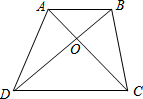 如图,梯形ABCD中,AB∥CD,AB=2,CD=3,若S△AOB=1,则S梯形ABCD=$\frac{25}{4}$.
如图,梯形ABCD中,AB∥CD,AB=2,CD=3,若S△AOB=1,则S梯形ABCD=$\frac{25}{4}$.
分析 由梯形ABCD中,AB∥CD,可得△AOB∽△COD,然后由相似三角形的对应边成比例,证得$\frac{OA}{OC}=\frac{OB}{OD}=\frac{AB}{CD}$=$\frac{2}{3}$,又由相似三角形面积的比等于相似比的平方,等高三角形面积的比等于其对应底的比,即可求得△COD,△AOD与△BOC的面积,继而求得答案.
解答 解:∵梯形ABCD中,AB∥CD,
∴△AOB∽△COD,
∵AB=2,CD=3,
∴$\frac{OA}{OC}=\frac{OB}{OD}=\frac{AB}{CD}$=$\frac{2}{3}$,
∴S△AOB:S△COD=4:9,S△AOB:S△AOD=OB:OD=2:3,S△AOB:S△BOC=OA:OC=2:3,
∵S△AOB=1,
∴S△COD=$\frac{9}{4}$,S△AOD=S△BOC=$\frac{3}{2}$,
∴S梯形ABCD=S△AOB+S△COD+S△AOD+S△BOC=1+$\frac{9}{4}$+$\frac{3}{2}$+$\frac{3}{2}$=$\frac{25}{4}$.
故答案为:$\frac{25}{4}$.
点评 此题考查了梯形的性质以及相似三角形的判定与性质.注意掌握各三角形的面积关系是解此题的关键.

练习册系列答案
相关题目
20.下列图象中,表示直线y=-x+1的是( )
| A. |  | B. |  | C. |  | D. |  |
2. 如图是2012年10月份的日历表,任意圈出一竖列上相邻的三个数.请你运用方程思想来研究,发现这三个数的和不可能是( )
如图是2012年10月份的日历表,任意圈出一竖列上相邻的三个数.请你运用方程思想来研究,发现这三个数的和不可能是( )
 如图是2012年10月份的日历表,任意圈出一竖列上相邻的三个数.请你运用方程思想来研究,发现这三个数的和不可能是( )
如图是2012年10月份的日历表,任意圈出一竖列上相邻的三个数.请你运用方程思想来研究,发现这三个数的和不可能是( )| A. | 69 | B. | 54 | C. | 27 | D. | 40 |
 “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h(约为19.4m/s).如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方40m的C处(即AC=40m),过了2s后,行驶到B处,测得小汽车与车速检测仪间距离AB为50m,问:这辆小汽车超速了吗?
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h(约为19.4m/s).如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方40m的C处(即AC=40m),过了2s后,行驶到B处,测得小汽车与车速检测仪间距离AB为50m,问:这辆小汽车超速了吗?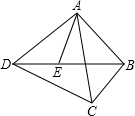 E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE. 如图,已知D为△ABC的内心,∠A=m,∠D=n,请你探究m、n之间的关系,并证明你的结论.
如图,已知D为△ABC的内心,∠A=m,∠D=n,请你探究m、n之间的关系,并证明你的结论.