题目内容
7．
已知二次函数y=-x2+2x+3．（1）用配方法将y=-x2+2x+3化成y=a（x-h）2+k的形式；
（2）在平面直角坐标系中，画出这个二次函数的图象；
（3）当x取何值时，y随x的增大而减少；
（4）当x取何值时，y＜0．
分析 （1）运用配方法把一般式化为顶点式；
（2）根据函数图象的画法画出二次函数图象即可；
（3）根据二次函数的性质解答即可；
（4）运用数形结合思想解答即可》
解答 解：（1）y=-x2+2x+3=-（x-1）2+4；
（2）这个二次函数的图象如图：
（3）x≥1时，y随x的增大而减少；
（4）x＜-1或x＞3时，y＜0．
点评 本题考查的是二次函数的三种形式、二次函数的性质，掌握配方法把一般式化为顶点式是解题的关键．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
17．若x＜y成立，则下列不等式一定成立的是（ ）
| A． | 4x＜3y | B． | -x＜-y | C． | $\frac{x}{5}$＞$\frac{y}{5}$ | D． | x-2015＜y-2015 |
2．
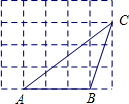如图，在5×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则sinA的值为（ ）
如图，在5×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则sinA的值为（ ）| A． | 1 | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
已知二次函数的解析式是y=x2-2x-3
19．下列语句不是命题的是（ ）
| A． | 延长AB到D，使BD=$\frac{1}{3}$AB | B． | 两点之间线段最短 | ||
| C． | 两条直线相交有且只有一个交点 | D． | 等角的补角相等 |