题目内容
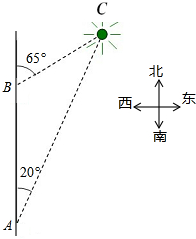 如图,一艘船以每小时32海里的速度向正北航行,在A处观察到灯塔C在船的北偏东20°方向上,半个小时后船航行到B处,在B处观测到灯塔C在船的北偏东65°的方向上.求灯塔C与B处之间的距离.
如图,一艘船以每小时32海里的速度向正北航行,在A处观察到灯塔C在船的北偏东20°方向上,半个小时后船航行到B处,在B处观测到灯塔C在船的北偏东65°的方向上.求灯塔C与B处之间的距离.考点:解直角三角形的应用-方向角问题
专题:
分析:首先作BD⊥AC于点D,进而得出△CDB为等腰直角三角形,再利用等腰直角三角形的性质求解即可.
解答: 解:作BD⊥AC于点D,
解:作BD⊥AC于点D,
∵以每小时32海里的速度向正北航行,半小时后航行到B处,
∴AB=16×
=8海里,
∵∠BAC=20°,
∴BD=AB•sin20°≈2.74海里,
∵在B处观测到灯塔C在船的北偏东65°的方向上,
∴∠C=65°-20°=45°,
∴BC=
BD≈1.414×2.74≈3.9海里,
∴灯塔C与B处之间的距离.
 解:作BD⊥AC于点D,
解:作BD⊥AC于点D,∵以每小时32海里的速度向正北航行,半小时后航行到B处,
∴AB=16×
| 1 |
| 2 |
∵∠BAC=20°,
∴BD=AB•sin20°≈2.74海里,
∵在B处观测到灯塔C在船的北偏东65°的方向上,
∴∠C=65°-20°=45°,
∴BC=
| 2 |
∴灯塔C与B处之间的距离.
点评:此题主要考查了方向角问题的应用,根据已知得出△CDB为等腰直角三角形以及在直角三角形中求出AC的长是解题关键.

练习册系列答案
相关题目
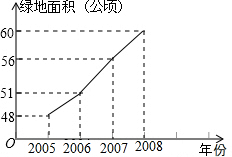 某城区近几年通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加.
某城区近几年通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加.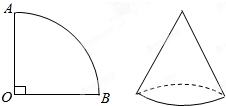 如图,已知扇形OAB的圆心角为90°,半径为4厘米,用这个扇形卷成的圆锥的侧面,求该圆锥圆锥的侧面积及圆锥的高.
如图,已知扇形OAB的圆心角为90°,半径为4厘米,用这个扇形卷成的圆锥的侧面,求该圆锥圆锥的侧面积及圆锥的高.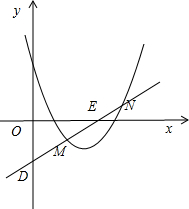 如图,已知抛物线y=x2-4x+3,过点D(0,-
如图,已知抛物线y=x2-4x+3,过点D(0,-