题目内容
16．一个三位数，百位数字是a，十位数字是b，个位数字是c，把百位数字a与个位数字c交换位置后，所得的新数与原数作差．试说明这个差能被99整除．分析 由题可得原数为100a+10b+c，新数为100c+10b+a，运用整式的加减法则，可得新数-原数=99（c-a），问题得以解决．
解答 证明：原数=100a+10b+c，新数=100c+10b+a，
则新数-原数=（100c+10b+a）-（100a+10b+c）
=100c+10b+a-100a-10b-c
=99c-99a
=99（c-a）．
∵c、a都是整数，
∴c-a是整数，
∴新数与原数的差能被99整除．
点评 本题主要考查多位数的表示，整式的加减法则、提取公因式，整除问题，将多项式转化为99的整数倍，是解决本题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
6．已知E是矩形ABCD的边BC上一点，BE＜CE，且AE⊥DE，AB=2，AD=5，那么S△ABE：S△CDE：S△ADE等于（ ）
| A． | 1：2：$\sqrt{5}$ | B． | 1：4：5 | C． | 2：4：5 | D． | 3：4：5 |
已知一个礼品盒的长、宽、高分别是12cm，8cm，2cm．现有4盒礼品，用下列两种方式包装．请问：哪种方式更省包装纸？
5．下列判断正确的是（ ）
| A． | 方程是等式，等式就是方程 | B． | 方程是含有未知数的等式 | ||
| C． | 方程的解就是方程的根 | D． | 方程2x=3x没解 |
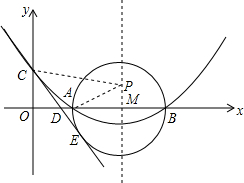如图，已知抛物线的对称轴为直线l：x=4，且与x轴交于点A（2，0），与y轴交于点C（0，2）．