题目内容
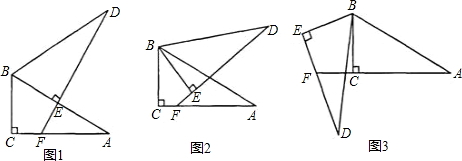
两个全等的直角三角形ABC和DEF重叠在一起,其中AB=2,AC=1.固定△ABC不动,将△DEF进行如下操作:(1)如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积;
(2)如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

分析:(1)根据平移的性质,可得AD=BE,CF∥BD.所以三角形ACD的面积等于三角形BEF的面积,则梯形的面积就等于直角三角形ABC的面积;
(2)根据直角三角形一边上的中线等于斜边的一半,以及平移的性质可以证明该四边形的四条边相等,则该四边形是菱形.
(2)根据直角三角形一边上的中线等于斜边的一半,以及平移的性质可以证明该四边形的四条边相等,则该四边形是菱形.
解答:解:(1)根据平移的性质得到:AD=CF=BE.CF∥BD.
∴?ACFD与?BCFE的底边相等,且高相等,
∴S?ACFD=S?BCFE,
又∵CD与BF分别为两平行四边形的对角线,
∴S△ACD=S△FCD=S△CFB=S△EFB,
∴S△ACD=S△BEF.
∵在Rt△ABC中,AB=2,AC=1,
∴∠ABC=30°,
∴BC=
=
,
∴S梯形CDBF=S△ABC=
×1×
=
;
(2)在直角三角形ABC中,AD=BD,则CD=BD,
根据平移的性质,得CF=BD,CD=BF,
∴CD=BD=CF=BF,
∴四边形CDBF是菱形.
∴?ACFD与?BCFE的底边相等,且高相等,
∴S?ACFD=S?BCFE,
又∵CD与BF分别为两平行四边形的对角线,
∴S△ACD=S△FCD=S△CFB=S△EFB,
∴S△ACD=S△BEF.
∵在Rt△ABC中,AB=2,AC=1,
∴∠ABC=30°,
∴BC=
| AB2-AC2 |
| 3 |
∴S梯形CDBF=S△ABC=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
(2)在直角三角形ABC中,AD=BD,则CD=BD,
根据平移的性质,得CF=BD,CD=BF,
∴CD=BD=CF=BF,
∴四边形CDBF是菱形.
点评:熟悉平移的性质和直角三角形的性质.注意:两条平行线间的距离处处相等.

练习册系列答案
相关题目

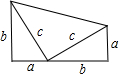 曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为
曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为