题目内容
 曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为
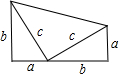
曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为分析:因为梯形的上底为a,下底为b,高为(a+b),则它的面积可表示为
(a+b)•(a+b);此梯形的面积还可以看成是三个直角三角形的面积和,即
(ab×2+c2);则
(a+b)(a+b)=
(ab×2+c2).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由题可知梯形面积为
(a+b)(a+b);
此梯形的面积还可以看成是三个直角三角形的面积和,即
(ab×2+c2).
因此
(a+b)(a+b)=
(ab×2+c2)
即a2+b2=c2.
| 1 |
| 2 |
此梯形的面积还可以看成是三个直角三角形的面积和,即
| 1 |
| 2 |
因此
| 1 |
| 2 |
| 1 |
| 2 |
即a2+b2=c2.
点评:主要应用了梯形的面积公式和三角形的面积公式.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为________,又可以表示为________.对比两种表示方法可得________.化简,可得a2+b2=c2.他的这个证明也就成了数学史上的一段佳话.
曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为________,又可以表示为________.对比两种表示方法可得________.化简,可得a2+b2=c2.他的这个证明也就成了数学史上的一段佳话.